고정 헤더 영역
상세 컨텐츠
본문
삼각함수 특수각 표
삼각함수 계산시 자주 쓰이는 각도는 0도, 30도, 45도, 60도, 90도 입니다.
이 각도들을 특수각이라고 하고,
이 특수각에 대한 삼각함수 값은 문제에서 일일이 값을 가르쳐주지 않기 때문에 잘 외워둬야 합니다.
특수각에 대한 삼각함수값을 표로 정리하면 아래와 같습니다.

삼각함수 특수각 증명
삼각함수의 특수각이 나오게 된 이유는 특수각들이 직각삼각형에서 많이 쓰이는 각이기 때문입니다.
i) sin45˚, cos45˚, tan45˚ 의 증명
sin45˚, cos45˚, tan45˚ 의 증명 직각이등변삼각형을 토대로 쉽게 증명 가능합니다.
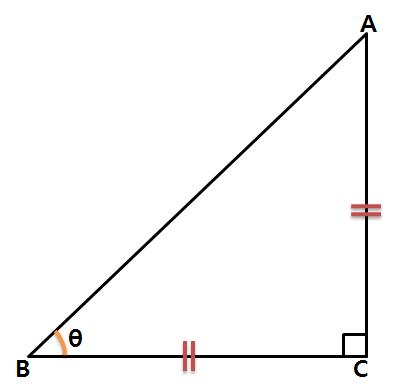
위 직각 이등변 삼각형에서 선분 BC의 길이(=선분AC의 길이)를 1로 보면,
빗변AB의 길이는 피타고라스의 정리를 이용해 구할 수 있습니다.


위 그림으로부터 45˚에 관한 삼각비를 구할 수 있습니다.
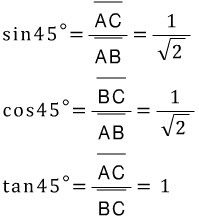
ii) sin30˚, cos30˚, tan30˚ 및 sin60˚, cos60˚, tan60˚의 증명
sin30˚, cos30˚, tan30˚및 sin60˚, cos60˚, tan60˚의 증명은
반원의 원주각 및 외각의 성질로 증명 가능합니다.

위 그림은 두 내각이 각각 30˚와 60˚인 직각삼각형과 그 외접원입니다.
직각삼각형의 외심(외접원의 중심)은 직각삼각형 빗변의 중점이라는 게 알려져있습니다.
따라서 외심 O는 점 A와 B의 중점입니다.
또한 선분 OA, OB, OC는 모두 외접원의 반지름으로 모두 같습니다.
(반지름의 길이를 임의로 1로 두겠습니다.)

삼각형 OBC는 이등변 삼각형이 되는군요. 따라서 ∠OBC와 ∠OCB는 30˚로 서로 같습니다.
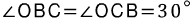
한편, ∠COA는 삼각형OBC의 외각으로, ∠OBC와 ∠OCB의 합과 같습니다.

이를 그림으로 나타내면 아래와 같습니다.

삼각형 AOC를 보면 ∠OAC=∠AOC=∠OCA=60˚인 정삼각형이 됩니다.
따라서 변AC는 외접원의 반지름인 1과 같습니다.
원래의 직각삼각형 ABC를 보면, 빗변인 AB의 길이가 2, 높이인 AC의 길이가 1임을 알 수 있습니다.
피타고라스의 정리를 쓰면 밑변 BC의 길이를 구할 수 있습니다.

정리하면 다음 그림처럼 되고,

그림으로부터 sin30˚, cos30˚, tan30˚ 및 sin60˚, cos60˚, tan60˚ 를 구할 수 있습니다.


증명 완료//
특수각에 대한 삼각함수 값 정도는 외워둬야 실전에 활용할 수 있습니다.
단순한 암기도 중요하지만 왜 그런 값이 나오는지에 대해 고민해보고 위의 방식처럼 유도해보는 것도 좋은 공부방법이라 할 수 있겠습니다.
'고등수학' 카테고리의 다른 글
| 삼각형 공식 정리(직각삼각형 닮음 공식/파푸스의 중선 정리/내,외각의 이등분선 공식) (0) | 2021.02.27 |
|---|---|
| 역함수의 모든 것 - 역함수의 정의/개념/성질/미분/적분 (1) | 2021.02.27 |
| 삼각형의 무게중심에 관한 공식, 증명, 성질 (2) | 2021.02.27 |
| 삼각형 사인 법칙 증명 (0) | 2021.02.27 |
| 삼각형의 외심 공식, 증명, 성질 (0) | 2021.02.27 |




