고정 헤더 영역
상세 컨텐츠
본문
삼각형 공식 정리
- 직각삼각형 닮음 공식/파푸스의 중선 정리/내,외각의 이등분선 공식
이 포스팅은 중3때 나오는 삼각형 공식 정리 및 그 유도에 관한 글 입니다.
직각삼각형의 닮음은 도형 관계에서 종종 등장하는 내용이라 꼭 이해하고 있어야 합니다.
그 외 파푸스의 중선정리, 외각과 내각의 이등분선 관련 공식도 가끔 출제되곤 합니다.
이에 관한 공식 유도 및 식의 의미를 정리해서 전달하면 많은 학생들에게 도움이 되지 않을까하여 이렇게 글을 씁니다.
이 글이 필요한 학생은
1. 직각삼각형의 닮음 공식과 그 유도가 궁금한 학생
2. 파푸스의 중선정리 공식 및 그 유도가 궁금한 학생
3. 삼각형 내각의 이등분선의 공식 및 그 유도가 궁금한 학생
4. 삼각형 외각의 이등분선의 공식 및 그 유도가 궁금한 학생
5. 중학교 도형을 소홀히 한 학생
입니다.
삼각형 관련 공식
1) 직각삼각형 닮음 공식

위와 같은 직각 삼각형에서, 아래 네가지 관계가 성립합니다.

2) 파푸스의 중선 정리
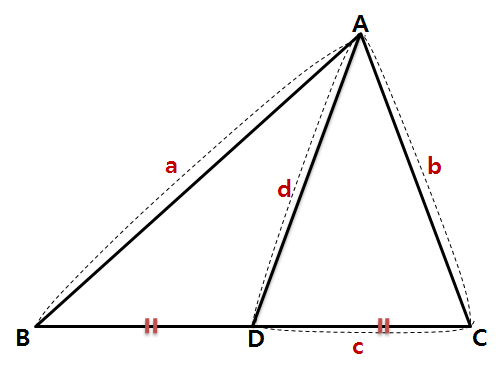
위와 같이 임의의 삼각형의 중선을 그었을 때, 다음 식이 성립합니다.

3) 내각의 이등분선 공식
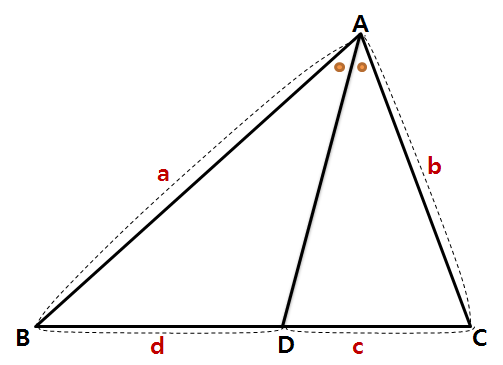
위와 같이 삼각형의 한 내각(여기선 ∠A)의 이등분선을 그었을 때, 아래 관계가 성립합니다.
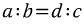
4) 외각의 이등분선 공식

위와같은 삼각형 ABC에서 한 외각(여기선 ∠A의 외각)을 그었을 때 다음 관계가 성립합니다.

공식 유도
1) 직각삼각형의 닮음 공식 유도

-내각들의 관계 설정
먼저, 각각의 내각의 관계를 알아봅시다.
(큰 직각삼각형 ABC에서) ∠ABC를 임의로 ●라 하고 ∠ACB를 임의로 x 라 해봅시다.
삼각형의 내각의 합은 180˚ 이기 때문에 직각삼각형에서 나머지 두 내각의 합은 90˚입니다.
따라서, ● + x = 90˚
한편, 작은 직각삼각형 ACD에서 두 내각 ∠CAD와 ∠ACD의 합 역시 90˚가 돼야합니다.
그런데 ∠ACD를 아까 x 라 표시했으므로, ∠CAD는 필연적으로 ●가 되어야합니다.
(∵∠CAD = 90˚ - ∠ACD = 90˚ - x = ●)
이제 ∠BAD만 남았는데요. 공교롭게도 ∠BAD와 앞에서구한 ∠CAD와의 합이 90˚가 되는군요.(그림)
따라서 ∠BAD는 다시 x 로 표현할 수 있습니다.
(∵∠BAD = 90˚ - ∠CAD = 90˚ - ● = x )
이를 종합하면 아래와 같은 그림처럼 됩니다.

-닮은 삼각형을 찾아 닮음비 구하기
이제 닮은 삼각형들을 찾아서 닮음비를 구해봅시다.
모든 내각들이 직각(⊥), ●, x 로 표현돼있으므로 그림에서 보이는 세 삼각형들(ABC, ABD, ACD)은 모두 닮은 직각삼각형들입니다.
이 때 대응하는 변들을 찾아 그 닮음비를 표현하면 됩니다.
대응하는 변을 찾을 때에는 변에 포함된 각을 똑같이 대응시키면 됩니다.
i) 삼각형 ABD와 삼각형 ABC
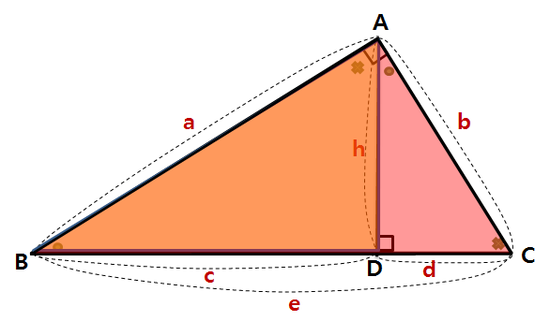
중간 크기의 삼각형 ABD와 전체 크기의 삼각형 ABC를 봅시다.
삼각형ABD에서 선분 a에 대응하는 삼각형ABC의 선분은 e가 됩니다.
(선분 a를 잘 보면, 양 끝에 각 ●와 x 가 포함돼있습니다. 큰 삼각형 ABC에서 이에 해당하는 변을 찾으면 e가 됩니다. 선분 e의 양 끝에도 ●와 x 가 있죠. 앞으로 계속 이런 논리를 적용해서 대응하는 변을 찾을 것입니다.)
다시, 삼각형 ABD에서 선분 c에 해당하는 삼각형 ABC의 선분은 a가 됩니다.
(삼각형 ABD에서 선분 c는 각 ●와 직각(⊥)을 포함하는 변입니다. 큰 삼각형에서 이 두 각들을 포함하는 변은 선분 a가 됨을 알 수 있습니다.)
따라서, 다음 비례식

을 세울 수 있고, 이를 풀면 a² = ce, 첫번 째 공식을 얻습니다.

ii) 삼각형 ACD와 삼각형 ABC
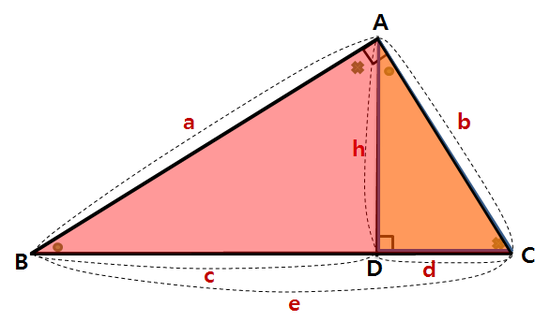
작은 삼각형 ACD와 전체 삼각형 ABC를 봅시다.
삼각형 ACD에서 변 b에 대응하는 삼각형 ABC의 선분은 e입니다. (각 ●와 x)
삼각형 ACD에서 변 d에 대응하는 삼각형 ABC의 선분은 b입니다. (각 x와 직각⊥)
따라서 다음 비례식

을 세울수 있고, 이를 풀면 두 번째 공식을 얻습니다.
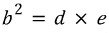
iii) 삼각형 ABD와 삼각형 ACD
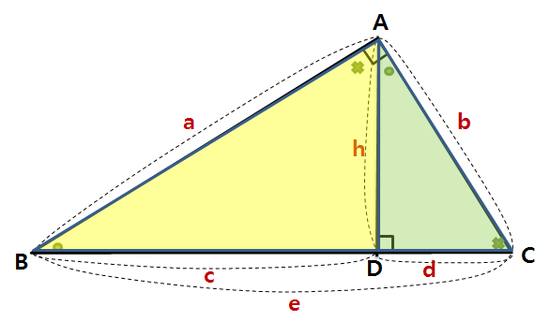
이제 작은 두 삼각형 ABD와 ACD의 닮음비를 구해봅시다.
삼각형 ABD에서 변 c에 대응하는 삼각형 ACD의 선분은 h입니다. (각 ●와 직각⊥)
삼각형 ABD에서 변 h에 대응하는 삼각형 ACD의 선분은 d입니다. (각 x와 직각⊥)
따라서 다음 비례식

을 세울 수 있고, 이를 풀면 세 번째 공식을 얻습니다.

iv) 삼각형의 ABC의 넓이(소자 공식)
마지막 공식은 삼각형 ABC의 넓이를 서로 다른 방법으로 표현함으로써 얻을 수 있습니다.
삼각형 ABC에서 밑변을 b, 높이를 a로 보면 넓이는 1/2 x a x b 가 됩니다.
삼각형 ABC에서 밑변을 e, 높이를 h로 보면 넓이는 1/2 x e x h 가 됩니다.
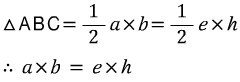
이 공식은 모양상 소자 공식으로도 알려져있죠.

2) 파푸스의 중선 정리 공식 유도
파푸스의 중선정리는 코사인 제 2법칙으로 유도할 수 있습니다.
코사인 제 2법칙의 공식 및 유도가 궁금한 분은 아래 링크를 참고하세요.
아래 그림에서 작은 삼각형 ABD에 주목해봅시다.
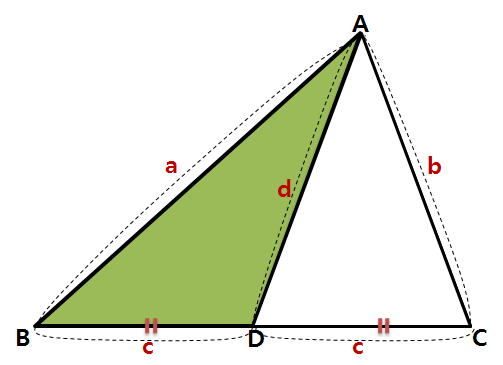
삼각형 ABD에서 코사인 B는 세 변 a, c, d로 표현할 수 있습니다.

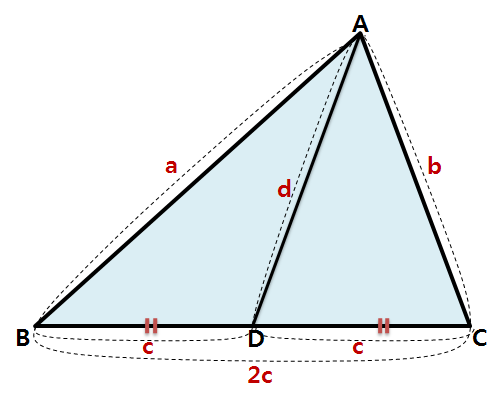
한편, cosB는 큰 삼각형 ABC의 변을 통해서도 구할 수 있습니다.
전체 삼각형 ABC의 각 변 a, 2c, b를 통해 cosB를 표현하면 다음과 같습니다.
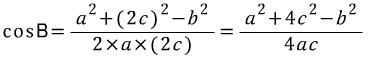
이 식을 위에서 구한 식과 연결하면 파푸스가 이끌어낸 중선정리의 결과를 얻을 수 있습니다.

3) 내각의 이등분선 공식 유도
아래 그림과 같이 삼각형 ABC에서 내각의 이등분선 AD와 평행한 직선을 긋고,
그 직선이 선분 AB의 연장선과 만나는 점을 E라 합시다.
(원래 삼각형은 검은색 실선, 보조선은 파란색 실선으로 표현했습니다.)

∠DAC와 ∠ACE는 엇각으로 같습니다.
∠BAD와 ∠AEC는 동위각으로 같습니다.
따라서, 삼각형 ACE는 두 밑각이 서로 같은 이등변 삼각형이며, 선분 AC와 선분 AE의 길이가 b로 서로 같습니다. (아래 그림)

위 그림에서 삼각형 BAD와 삼각형 BEC는 모든 내각이 같은, 서로 닮은 삼각형입니다.
또한 평행선의 관계에 의해서 다음 비례식이 성립합니다.
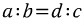
유도는 보조선을 그어서 했으나, 보조선이 없는 원래 그림, 즉 삼각형 ABC(검은 실선)와 한 내각의 이등분선이 주어진 그림에서 위 비례식을 생각해 낼 수 있어야 합니다.
3) 외각의 이등분선 공식 유도
아래 그림과같이 삼각형 ABC에서 한 점 C로부터 ∠A의 외각의 이등분선과 평행한 직선을 긋고,
그 직선이 선분 AB와 만나는 점을 E라 둡시다.
(내각의 이등분선 공식을 유도할 때랑 똑같은 아이디어입니다. 위에서도 내각의 이등분선과 평행한 평행선을 그어서 생각했습니다.)
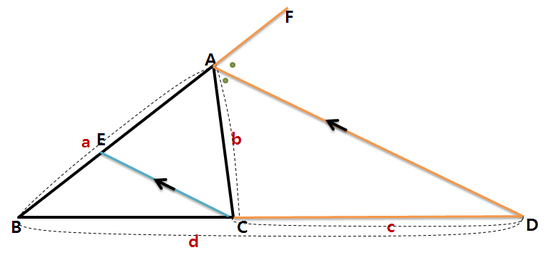
위 그림에서 파란색 선분 EC는 보조선입니다.
두 평행선으로부터 동위각 및 엇각의 관계를 얻어낼 수 있습니다.
∠DAC=∠ACE (엇각)
∠DAF=∠CEA (동위각)
따라서 삼각형 ACE는 두 밑각이 서로 같은 이등변삼각형이고, 따라서 선분 AE와 AC는 길이가 b로 서로 같습니다. (아래 그림)
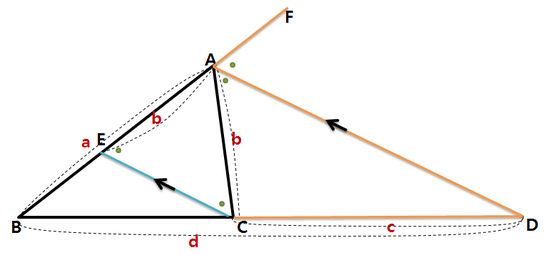
위 그림에서 삼각형 BCE와 삼각형 BDA는 세 내각이 모두 같은 닮은 삼각형입니다.
또한, 평행선의 관계에 의해서 아래와 같이 각 선분들끼리 일정한 닮음비가 성립합니다.
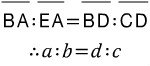
공식유도는 보조선을 그어서 했으나,
보조선이 없는 원래 상황에서도 위 비례식을 쓸 수 있어야 합니다.
유도 완료//
정리
이번 포스팅에서는
삼각형의 몇 가지 공식에 대해 다뤄봤습니다.
-직각삼각형의 닮음 공식
-파푸스의 중선정리
-삼각형의 한 내각의 이등분선
-삼각형의 한 외각의 이등분선
이 내용은 모두 중학교 때 나오는 공식으로, 유도과정이 그리 복잡하지 않기 때문에 한 번 쯤은 직접 유도해볼만한 것들입니다.
설령 정확한 공식이 기억이 나지 않는다 하더라도, 곧바로 공식을 유도해서 써먹을 수 있을 것입니다. 따라서 반드시 직접 위 공식들을 유도해보시기 바랍니다.
직접 해 본 학생과 그러지 않고 대충 눈대중으로만 익힌 학생의 격차는 상당히 큽니다.
제 글이 많은 학생들에게 도움이 됐으면 합니다.
'고등수학' 카테고리의 다른 글
| 절댓값이 포함된 함수의 그래프 (0) | 2021.02.27 |
|---|---|
| 원 관련 공식 정리 및 유도(원의 내접, 원의 외접, 원의 접선, 원주각, 원의 할선) (1) | 2021.02.27 |
| 역함수의 모든 것 - 역함수의 정의/개념/성질/미분/적분 (1) | 2021.02.27 |
| 삼각함수 특수각 표 및 증명 (1) | 2021.02.27 |
| 삼각형의 무게중심에 관한 공식, 증명, 성질 (2) | 2021.02.27 |




