고정 헤더 영역
상세 컨텐츠
본문
::지수함수의 미분, 자연로그의 미분 증명::
- (e^x-1)/x, e^x, a^x, ln(x), loga(x)
이 포스팅은 지수함수의 미분(e^x-1/x, e^x), 자연로그(lnx)의 미분에 관한 글 입니다.
자연상수는 파이(pi)와 함께 거론되는 대표적인 무리수로, 자연상수의 지수함수의 극한, 미분과 적분파트에서 자주 등장합니다. 지수함수의 미분은 대학교때 배우는 미분방정식까지 확장되기 때문에 매우 중요한 부분입니다. 따라서 자연상수의 개념과 그로부터 파생되는 지수함수의 극한, 미분, 로그함수의 미분까지 전반적인 내용을 알아놓는 게 중요합니다.
이 글이 필요한 학생은
1. 자연상수의 정의 및 관련 극한이 궁금한 학생.
2. 지수함수의 미분이 궁금한 학생.
3. 로그함수의 미분이 궁금한 학생.
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
그럼 포스팅 시작합니다.
자연상수(e)의 정의와 극한
- 자연상수의 정의
자연상수(e)는 17세기 수학과 과학이 발달함에따라 자연스레 등장한 개념으로, 1618년 John Napier라는 수학자의 논문에 처음 등장했으며(이 논문에서는 e를 주로 다룬 건 아니고 Appendix에서 e 로그 값을 간접적으로 첨부한 수준), 이후 베르누이(Jacob Bernoulli)라는 사람에의해 자연상수 e의 정의와 그 대략적인 값(2.71828...)이 유도됩니다.

그러나 자연상수 e의 중요성을 학문적으로 발전시킨 사람은 다름아닌 18세기의 수학자 오일러(Leonhard Euler)였습니다. 그는 e의 성질을 이용해 복소수 영역에서 유명한 오일러 공식(Euler's formula)을 유도합니다.

오일러의 이런 지대한 공을 기려 자연상수 e를 오일러넘버(Euler's number)라고도 부릅니다.
- 자연상수의 관련 극한 (e^x-1)/x
고교 수학에서는 지수함수나 로그함수의 미분을 유도할 때 꼭 다음 자연상수의 극한을 이용합니다.

이 극한은 마치 삼각함수에서 x가 0으로 갈 때 sinx/x 의 극한값이 1이라는 것에 대응하는, 지수, 로그파트의 기본 극한입니다. 증명은 자연상수 e의 정의로부터 이끌어낼 수 있습니다.
먼저 e^x-1을 t로 치환합니다(t=e^x-1).
그러면 x가 0으로 갈 때 t역시 0으로 가며, x를 다시 t에 대해 정리하면 x=ln(1+t)가 됩니다. (ln은 밑이 e인 로그를 나타냅니다.) 이를 주어진 식에 적용하면 아래와 같이 식을 전개할 수 있습니다.

증명완료//
지수함수(e^x, a^x)의 미분, 로그함수(lnx, logax)의 미분
- 자연상수의 지수함수(y=e^x)의 미분
앞으로 나오게 될 모든 공식들은 e^x의 미분공식으로부터 출발합니다. 따라서 e^x의 미분 공식 및 유도과정을 제대로 익혀두는 게 좋습니다.
다음 도함수의 정의를 이용해서 f(x)=e^x를 미분해봅시다.

수식 전개 중간에 위에서 소개한 극한값(e^x-1/x)을 이용했습니다. 이처럼 e^x를 미분하면 (e의 정의의 특성상) 자기자신이 됩니다. 반대로 말하면 미분한 게 자기 자신이 되는 함수는 e^x입니다.
- 일반적 지수 함수 (y=a^x)의 미분
일반적인 지수함수의 미분의 경우, 다음 로그 관련 법칙을 이용해 밑을 e로만 변형시켜주면 됩니다.

공식이 어떻게 적용됐는 지 잘 파악하시기 바랍니다. (일반적으로 학생들이 로그에서의 밑변환공식은 잘 다루나, 지수의 밑을 변환할 때 위와같이 하는 걸 제대로 익히지 않고 있습니다.)
각설. 위에서 얻은 결과 a^x=e^(xlna) 를 가지고 미분을 완성시킬 수 있습니다.

위에서 적용한 건 다름아닌 합성함수의 미분입니다. 합성함수의 미분은 함수의 전체 형태를 먼저 미분한 후 안의 것을 한번 더 미분해서 곱해주면 되는 게 핵심입니다. 합성함수의 미분이 궁금한 분은 다음 링크를 참고하세요.
https://color-change.tistory.com/46
식을 정리하면 다음 공식을 얻을 수 있습니다.

앞에서 밑을 변형했던 항을 다시 원래 형태(a^x)로 복원했습니다.
증명완료//
- 자연로그(y=lnx)의 미분
자연로그함수의 미분 역시 도함수의 정의로부터 출발합니다. f(x)=lnx 로 두고 미분을 해봅시다.

수식전개 중간에 등장하는 자연상수 e의 개념에 주목하기 바랍니다.
자연상수의 정의(극한)에서 밑의 1과 더해지는 수와 지수에 있는 수가 역수관계만 성립하면 됩니다.

증명에서 ⊙에 해당하는 항은 x/h 였습니다. (식을 볼 줄 아는 안목이 필요하겠죠.)
- 일반적 로그함수(logax)의 미분
일반적인 로그함수의 미분은 다음 밑변환공식을 이용해 밑을 e로 맞춰주는 작업부터 출발합니다.
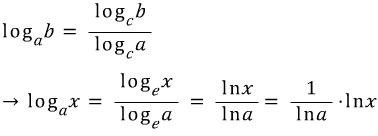
밑을 e로 맞춰준 이유는 위에서 구한 lnx의 미분을 이용하기 위함입니다.

공식유도 완료//
정리
이번 포스팅에서는
1. 자연상수의 정의 및 관련 극한
2. 지수함수의 미분
3. 로그함수의 미분
에 대해서 알아보았습니다.
지수함수 및 로그함수는 고등학교 이과(자연계열)에서 배우는 대표적인 초월함수로, 이들의 미분 및 적분을 다룰 줄 아는 게 중요합니다. 공식 중간에 lna, 1/lna 등이 나오는데 이를 무작정 암기하려고하면 암기도 잘 되지 않을뿐더러 후에 헷갈리기 쉽습니다. 따라서 공식유도를 통해 이러한 항들이 왜 나왔는지부터 차근차근 되짚어보는 게 중요합니다.
제 글이 많은 학생들에게 도움이 됐으면 좋겠습니다.
'고등수학' 카테고리의 다른 글
| 정사영의 정의/공식/고난이도 문제 (0) | 2021.06.19 |
|---|---|
| 정사면체 높이/부피 구하는 법(공식 유도) (2) | 2021.06.19 |
| 음함수의 미분 - 개념과 적용 (1) | 2021.04.02 |
| 삼각함수의 미분과 적분 (0) | 2021.04.02 |
| 삼각함수의 기본 극한 증명 (sinx/x, tanx/x) (6) | 2021.04.02 |




