고정 헤더 영역
상세 컨텐츠
본문
삼각함수의 기본 극한 증명 (sinx/x, tanx/x)
이 포스팅은 삼각함수의 기본 극한- sinx/x, tanx/x - 증명에 관한 글 입니다.
고등수학 자연계 수학2에 나오는 삼각함수의 극한 중 가장 기본이 되는 두 식이 있습니다. 바로, x가 0으로 갈 때의 두 함수 sinx/x, tanx/x의 극한이 1로 수렴한다는 것입니다. 이 두 식은 삼각함수의 극한을 구할 때 종종 등장하는 식으로, 정답에 이르기까지의 활용도 및 중요도가 매우 높습니다.
이번에는 이 두 식을 증명해보고, 로피탈의 정리와 비교해서 활용법을 소개하겠습니다.
이 글이 필요한 학생은
1. 삼각함수의 극한에서 기본식의 증명이 궁금한 학생
2. 삼각함수의 극한을 잘 활용하지 못하는 학생
3. 로피탈의 정리를 즐겨쓰나, 실전에서 관련 문제를 종종 틀리는 학생
4. 함수의 극한에 대해서 체계가 덜 잡힌 학생
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
그럼 포스팅 시작합니다.
삼각함수의 극한(기본식)
삼각함수의 극한에서 기본이 되는 두 식은 다음과 같습니다. 식에서 삼각함수에 들어있는 변수 x의 단위는 라디안(rad)입니다.
i) sinx/x
x가 0으로 갈 때, 함수 f(x)=sinx/x의 극한은 1로 갑니다.

함수 f(x)=sinx/x 에서 f(0)은 존재하지 않으며(분모에 0이 들어가면 안되죠.), f(x)를 좌표평면에 그래프로 나타내면 아래와 같습니다.

ii) tanx/x
x가 0으로 갈 때, 함수 f(x)=tanx/x의 극한은 1로 갑니다.

함수 f(x)=tanx/x 에서 f(0)은 존재하지 않으며(분모에 0이 들어가면 안되죠.), f(x)를 좌표평면에 그래프로 나타내면 아래와 같습니다.

삼각함수의 극한 기본식 증명
i) sinx/x
증명은 아래 그림의 도형 관계에서 출발합니다.
아래와 같이 반지름의 길이가 r, 중심각의 크기가 x인 부채꼴 AOB의 현 AB에 의해 생기는 내부의 삼각형을 AOB, 점 B에서의 접선과 선분 OA의 연장선의 교점을 C라 할 때, 이 때 생기는 직각삼각형을 COB라고 합시다. 그러면 한 변과 각이 주어졌을 때의 삼각비의 표현법에 따라, 선분 BC의 길이는 r*tanx가 됩니다. 이를 그림으로 표현하면 아래 그림과 같습니다.
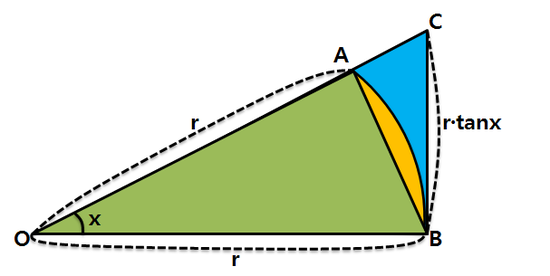
그림을 보면 삼각형 AOB의 넓이가 가장 작고, 다음으로 부채꼴 AOB, 삼각형 COB 순서로 넓이가 큼을 알 수 있습니다. 이를 수식으로 나타내면 다음과 같습니다.

여기서 삼각형 AOB의 넓이는 두 변과 그 끼인각이 주어졌을 때의 넓이공식으로 구했고, 부채꼴의 넓이는 x가 라디안일 때의 공식으로 표현했으며, 삼각형 COB의 넓이는 삼각형의 넓이의 정의를 이용해서 표현했습니다.
식에서 공통 부분인 1/2 r² 을 약분시켜주고, 각 변을 sinx로 나눕니다. 이 때, 0<x<π/2 이므로 sinx는 양수를 가지고, 따라서 부등호 방향은 바뀌지 않습니다.

위에서 tanx = sinx/cosx 라는 관계식을 적용해서 식을 정리했습니다. 이제 부등식에 나타난 항들(엄밀히 말하면 x에 관한 함수들)에 x->0의 극한을 취합니다.

샌드위치 정리에 의해 x가 0으로 갈 때의 함수 x/sinx 의 극한값은 1이라는 결과를 얻습니다. 우리가 구하려던 원래 함수의 극한값은 이 함수에 역수를 취한 함수의 극한값이므로, 마찬가지로 1이 됩니다.
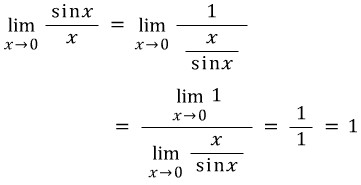
//증명 끝
ii) tanx/x
tanx/x 역시 앞에서 소개한 그림의 관계로부터 출발합니다. 두 삼각형과 부채꼴의 넓이를 x로 표현한 뒤 그 대소관계를 식으로 정리하는 데까지는 동일합니다.

이제 각 변을 tanx로 나눠봅시다.(위에서는 sinx로 나눴었습니다.) 이 때 0<x<π/2 이므로 tanx는 양수이고, 따라서 부등호 방향은 바뀌지 않습니다.

위에서 tanx = sinx/cosx 라는 관계식을 적용해서 식을 정리했습니다. 이제 부등식에 나타난 항들(엄밀히 말하면 x에 관한 함수들)에 x->0의 극한을 취합니다.

샌드위치 정리에 의해 x가 0으로 갈 때의 함수 x/tanx 의 극한값은 1이라는 결과를 얻습니다. 우리가 구하려던 원래 함수의 극한값은 이 함수에 역수를 취한 함수의 극한값이므로, 마찬가지로 1이 됩니다.

//증명 끝
정리
이번 포스팅에서는
1. 삼각함수의 기본 극한 증명
2. x가 0으로 갈 때 sinx/x의 극한값은 1이라는 공식 유도
3. x가 0으로 갈 때 tanx/x의 극한값은 1이라는 공식 유도
에 대해 알아보았습니다.
위에서 소개한 극한 공식 두 개는 수능을 준비하는 자연계 고등학생이라면 반드시 알아둬야 할 기본식입니다. 이들을 이용해서 복잡한 삼각함수의 극한을 구하는 경우가 많기 때문에 꼭 기억해둬야할 식입니다.
대부분의 극한에 관한 문제들은 로피탈의 정리를 이용하면 쉽게 풀리는 경우가 많습니다. 그러나, 평가원 모의고사나 수능같이 굵직한 시험에서는 단순히 로피탈의 정리만 적용해서는 문제를 해결할 수 없게끔 함수를 꼬아서 출제합니다.
따라서 교과과정에는 있지도 않은 로피탈의 정리만 기계적으로 적용하기 보다는, 기본적으로 배우게 되는 위 삼각함수의 극한을 적절히 이용해서 문제를 해결하는 습관을 기르는 게 중요하다고 생각합니다. 그러한 중요성을 상기시켜드리고자 이 글을 썼습니다.
제 글이 많은 학생들에게 도움이 됐으면 합니다.
'고등수학' 카테고리의 다른 글
| 음함수의 미분 - 개념과 적용 (1) | 2021.04.02 |
|---|---|
| 삼각함수의 미분과 적분 (0) | 2021.04.02 |
| 합성함수의 개념/정의/적용/미분 (0) | 2021.04.02 |
| (총정리) 삼각함수 관련 공식 (0) | 2021.04.02 |
| [증명] 다항함수 x^n의 미분 (1) | 2021.03.06 |




