고정 헤더 영역
상세 컨텐츠
본문
::합성함수의 개념/정의/적용/미분::
이 포스팅은 합성함수의 개념/정의/적용/미분에 관한 글 입니다.
합성함수는 복잡한 함수를 치환을 통해 간단히 나타내는 데 필요한 중요한 툴입니다.
복잡한 함수의 미분 역시 합성함수를 통해 쉽게 미분할 수 있는데요.
따라서 합성함수과 그 미분을 제대로 이해하고 활용하는 게 중요합니다.
이 글이 필요한 학생은
1. 합성함수의 개념이 잘 정립되지 않은 학생
2. 합성함수의 미분 공식 유도가 궁금한 학생
3. 합성함수의 미분을 적용할 때 그 개념이 헷갈리는 학생
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
그럼 포스팅 시작합니다.
2. 합성함수의 개념 및 그 적용
합성함수의 정의
합성함수는 두 함수 X→Y로의 함수와 Y→Z로의 함수를 하나의 함수인 X→Z로의 함수로 표현하는 것을 뜻합니다.

위 그림과 같이 X→Y로의 함수 y = f(x)와 Y→Z로의 함수 z = g(y)가 주어졌다고 칩시다.
우리는 위 그림 x에서 y를 거쳐 z로 가던 것을 중간단계(y)를 생략하고 곧바로 x에서 z로 보내는 함수 관계를 찾고자 합니다. (이를 함수를 합성한다고 하고, 합성함수를 g ο f 로 표현합니다. 가운데는 dot 표시입니다.)
어떻게 하면 될까요?
바로, 주어진 z = g(y) 에서 y에 y = f(x) 를 치환해서 대입하면 됩니다.
즉, 함수(값) z = g(y) = g(f(x)) 로 표현이 되겠죠.
다시 말해, g ο f = g(f(x)) 로 합성할 수 있습니다.
합성함수의 적용
이제 위 내용을 적용해봅시다.
인수분해할 때 다음과 같은 형태의 다항식
z = (x² - 2x)² - 2(x² - 2x) - 3
을 인수분해 해 본 경험이 있을 것입니다. (인수분해에서는 '식'이나, 여기선 이를 편의상 함수로 생각하겠습니다.)
i) 공통된 부분을 y라 치환하고,
ii) z 를 y에 관한 식으로 간단히 정리한 뒤 인수분해 하면 됩니다.
위 식에서 (x² - 2x) 를 y라 둡시다.(치환) y = x² - 2x
그러면 식은 아래와 같이 됩니다.
z = g(y) = y² - 2y -3
여기서 z = g(y)로 표현한 이유는, 식의 우변이 y에 관한 함수이기 때문입니다.
(사실 y가 x에 관한 식이기 때문에 (y = x² -2x) 전체적으로 보면 z = g(y) 역시 x에 관한 식입니다.)
y나 z나 모두 x에 관한 식이므로, 완전히 별개의 것이 아니라는 게 중요합니다.
이를 합성함수의 관점에서 보면 아래와 같이 표현할 수 있습니다.

위에서 z = (x² -2x)² -2(x² -2x) - 3 은, 사실 y = x² - 2x 를 거쳐 합성된 함수입니다.
이 때 합성된 결과를 다음과 같이 표현하는 것입니다.

z = g(f(x))의 의미는, x를 함수 y = f(x)에 집어넣고, 다시 함수 y=f(x)를 z=g(y)에 집어넣었다는 의미입니다.

(위 표기와 그림의 x→y→z 순서가 반대라는 점에 주의하세요.)
여기서 중요한 건, z는 x에 관해 표현되어있다는 것입니다. ( z = (x² -2x)² -2(x² -2x) - 3 )
복잡한 함수를 합성함수로 표현할 때, 무엇을 y = f(x)로 보고 무엇을 z = g(y)로 볼 것인가 하는 문제는, 합성함수의 정확한 개념이 없으면 헷갈릴 소지가 다분한 문제입니다.
결론을 말하면, 치환할 때 쓰이는 매개변수 y가 y = f(x)가 되고, 치환에 의해 매개화된 함수가 z = g(y) 가 됩니다.
문제에서
y = x² - 2x
z = y² - 2y - 3
이 되겠군요.
(여기서는 합성함수를 설명하는 게 목적이므로 나머지 인수분해 과정은 생략하겠습니다.)
3. 합성함수의 미분
합성함수의 미분 유도 과정
이제 z = g(f(x)) 의 의미를 알았으므로, 이를 미분에 적용해봅시다.
합성함수의 미분은 도함수의 정의를 적용하면 됩니다.
f(x)의 도함수는 아래와 같이 두 가지로 정의할 수 있습니다.

우리는 여기서 두 번째 정의(식의 맨 오른쪽)를 합성함수의 미분에 이용할 것입니다.
합성함수 z = g(f(x))의 도함수(미분)를 구해보면,

도함수의 '정의'를 이용하기 위해선 분모, 분자에 적절한 항을 곱해줘야합니다. (아래)

위 식의 왼쪽 항을 잘 보면, t가 x로 갈 때(극한 t→x ), 분모의 f(t)는 f(x)로 갑니다.(극한 f(t)→f(x) )

이 때 왼쪽 항은 z = g(y) = g(f(x))를 y 전체로 미분한 도함수(g'(y)) 이고, 오른쪽 항은 다름아닌 f(x)의 도함수의 정의입니다.

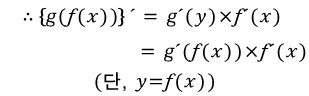
//유도완료
합성함수의 미분 적용
방금 전 유도한 합성함수의 미분법을 통해 처음에 예로 들었던 함수 z = (x² -2x)² -2(x² -2x) - 3 를 미분해봅시다.
이 함수는 y = x² - 2x 로 치환하면, 합성함수 z = y² - 2y -3 로 나타낼 수 있다고 했습니다.
즉, f(x) = x² - 2x , g(y) = y² - 2y -3 으로 볼 수 있는 합성함수 g(f(x)) 입니다.
이제 이를 미분해봅시다.

치환에 사용했던 매개변수 y를 x로 다시 환원해서 식을 완성시킬 수 있습니다.
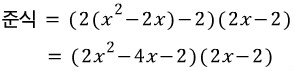
//끝
4. 정리
정리
이번 포스팅에서는
1. 합성함수의 개념과 그 적용,
2. 합성함수의 미분의 유도 과정과 그 적용
을 해보았습니다.
합성함수의 미분은 기계적으로 '문제풀이'에만 적용하면 한계가 있습니다.
합성함수의 정확한 개념과 왜 이런 개념이 나왔는지, 이 개념을 다른 문제에 어떻게 적용할 수 있을 지 고민한 학생과 그렇지 않은 학생은 후에 많은 격차를 보일 것입니다.
합성함수는 어떤 변수를 x, y, z로 볼 것인 지, 어떤 함수를 f, g로 볼 것인 지, 함수의 합성이 어떤 순서로 이루어진 것인 지, 다소 헷갈리는 부분입니다.
제 글을 통해 여러분이 합성함수의 정확한 개념을 잡는 데 조금이라도 도움이 됐으면 합니다.
부디 이 글뿐만아니라 다른 자료도 참고하시어 개념을 익히시길 바랍니다.
제 글이 많은 학생에게 도움이 됐으면 합니다.
'고등수학' 카테고리의 다른 글
| 삼각함수의 미분과 적분 (0) | 2021.04.02 |
|---|---|
| 삼각함수의 기본 극한 증명 (sinx/x, tanx/x) (6) | 2021.04.02 |
| (총정리) 삼각함수 관련 공식 (0) | 2021.04.02 |
| [증명] 다항함수 x^n의 미분 (1) | 2021.03.06 |
| [유형별 정리]경우의 수 - 함수의 개수 문제 (0) | 2021.03.06 |




