고정 헤더 영역
상세 컨텐츠
본문
거듭제곱근 개념 정리(a의 n제곱근, n제곱근 a)
1. 도입
거듭제곱근에 관한 개념은 중학교때 처음 다루기 시작하여 고등학교 수학1 지수 단원에서 심화 개념으로 등장합니다. 그런데 수능에서는 상대적으로 거듭제곱근보다는 지수법칙을 강조하여 이 부분을 잘 다루지 않는게 사실입니다. 내용이 워낙 기본적이고 다른 데에서도 출제해야할 내용이 많기 때문입니다.
그러다보니 학생들도 거듭제곱근의 개념을 소홀히 하고, 제대로 알고 넘어가지 않는 경향이 있는데요. 이번 2012년 6월 모의평가에서 거듭제곱근의 개념에 관한 문제가 무한등비급수와 맞물려 비중있게 출제된 바가 있어, 향후 수능에도 이 부분이 부각되지 않을까하여 미리 정리해보고자 합니다.
2. 개념
거듭제곱근, 즉 어떤 실수 a의 n제곱근이란, n제곱을 하여 a가 되는 모든 실수와 허수를 의미합니다.
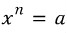
즉 위 방정식을 만족시키는 모든 x를 a의 n제곱근이라고 정의하는 것입니다. 방정식이 n차방정식이므로 일반적으로(a가 0이 아닐 때) 근의 개수는 n개이며, 이로부터 a의 n제곱근은 총 n개라는 사실을 알 수 있습니다. (중요)
→ a의 n제곱근은 총 n개
또한 위 방정식을 만족시키는 근은 실근도 있을 수 있고, 허근도 있을 수 있습니다. 실수와 허수를 아우르는 수체계를 복소수체계라고 하므로, a의 n제곱근을 복소수체계에서 헤아리면 실근과 허근이 합쳐 n개가 됩니다.
→ a의 n제곱근은 복소수체계에서 이해할 것. (실수, 허수)
한편, 거듭제곱근이 왜 거듭제곱"근"인지를 생각해보는 것도 좋은 학습입니다. 근이란 주어진 방정식을 만족시키는 x값으로, 소개한 n차 방정식에서는 x의 n거듭제곱이라는 형태로 주어지고 있습니다. 따라서 거듭제곱근이란 이름이 붙여진 이유는 그게 위 방정식을 만족시키는 "근"의 의미를 내포하고 있기 때문입니다. (기본)
→ a의 n제곱근은 방정식 「xⁿ=a」를 만족시키는 근
이제 예를 통해 실제 거듭제곱근의 형태를 파악해봅시다.
* 예제
1의 세제곱근을 구하라.
=> 1의 세제곱근이란, (위 정의에 따라) 어떤 수를 세번 곱해서 1이 되게하는 모든 수를 의미합니다. 즉, 다음 3차방정식의 모든 근이 됩니다.

위 방정식은 3차방정식으로, 근이 총 세 개가 존재합니다. 그들을 엄밀히 구해보면,

하나의 실근과 두 개의 허근이 나오는군요. 따라서 1의 세제곱근은 위 세 가지로 구할 수 있습니다.
(1의 세제곱근을 단순히 "³√1 = 1" 이라고 생각한 학생은 개념을 다시 한 번 확인하여 바로잡으시기 바랍니다. 참고로 세제곱근 1은 "³√1 = 1"이 되는데 이는 차후 설명할 예정입니다.)
3. 심화
이제 거듭제곱근에 대해 좀 더 깊이 알아봅시다. 앞서 말씀드렸다시피 거듭제곱근은 복소수 체계에서 이해해야한다고 했습니다. 즉, xⁿ=a 를 만족시키는 n개의 실근과 허근을 우리는 a의 n제곱근으로 받아들여야한다는 것이 위에서 소개한 핵심 내용입니다.
그러나 이를 실수에만 한정해서 생각할 필요가 있습니다. 왜냐하면 우리가 일반적으로 생각할 수 있는 수가 실수(=Real number)이며, 실제로도 수능에서도 허수는 거의 다루지 않기 때문입니다. 거듭제곱근 심화 내용은 사실 a의 n제곱근을 실수로 한정시켜 생각하는 것에 다름아닙니다. 앞으로 홀수 짝수, 양수 음수등 여러 기준으로 나눠 이를 생각해볼텐데, 방정식의 실근만 생각하겠다는 개념만 가져가면 헷갈릴 이유가 없다고 생각합니다.

a의 n제곱근을 구하는 위 n차방정식 중에서 실근만 구하려고하면 어떻게하면 될까요? 바로 방정식을 함수로 해석하는 것입니다, 다음과 같이.

주어진 방정식의 실근은 위 두 함수의 교점으로 나타날 것입니다. (우리가 x, y 좌표평면상에서 교점으로 점을 찍을 수 있다는 말은 그 점이 실수이기 때문에 가능한데요. 이처럼 방정식의 실근에 관한 문제에서 방정식을 함수로 해석하여 교점을 찾는 접근은 상당히 많이 쓰이기 때문에 알아두면 좋습니다.) 그런데 함수 y=xⁿ 그래프는 n이 홀수냐 짝수냐에 따라 모양이 달라지므로 홀짝을 기준으로 나눠서 생각할 필요가 있습니다.
i) n이 홀수일 때
n이 홀수일 때 y=xⁿ은 기함수가 되고 따라서 원점 대칭인 함수가 됩니다. 이 때 함수는 원점 (0, 0)과 두 정점 (1, 1), (-1, -1)을 항상 지난다는 특징이 있습니다.
ⓐ a가 양수일 때
n이 홀수이고 a가 양수이면, 좌표평면상에서 두 함수 y=xⁿ과 y=a는 아래 그림과 같이 나타납니다.

교점이 하나 존재하므로 이 경우에 a의 n제곱근중 실수인 것은 하나가 됩니다. (그것을 어떻게 표기할 것인지는 나중에 다룰텐데, 미리 언질을 드리자면 ⁿ√a로 표기합니다.)
ⓑ a가 0일 때
이 경우 좌표평면 상에서 그림은 아래와 같이 나타납니다.

교점의 개수는 역시 하나이며, 교점은 원점 O(0, 0)으로 주어집니다. 따라서 n이 홀수일 때 0의 n제곱근 중 실수인 것은 0이 됩니다.
ⓒ a가 음수일 때
a가 음수일 때 두 그래프의 교점을 그려보면 아래와 같습니다.

교점의 개수는 하나로 나오며, 이로부터 n이 홀수이고 a가 음수인 경우 거듭제곱근 중 실수인 것은 딱 하나 존재한다는 걸 이끌어낼 수 있습니다.
ⓓ n제곱근 a
위에서 ⓐ,ⓑ,ⓒ 세 경우 a의 부호에 상관없이 모두 그래프의 교점이 하나로 나타났습니다. 그 이유는 n이 홀수인 경우 함수 y=xⁿ이 원점대칭인 기함수가 되어 상수함수 y=a 그래프와 오직 한 점에서 만나기 때문인데요. 따라서 a의 부호에 상관없이 그 교점을 ⁿ√a로 쓰기로 약속한다면, (n이 홀수인 경우) a의 n제곱근중 실수인 것을 하나의 표기(=ⁿ√a)로 표현할 수 있습니다. 이제부터 그 표기를 "n제곱근 a"라고 읽기로 약속합니다.

따라서 n제곱근 a란, (n이 홀수라면) a의 n제곱근 중 그 값이 실수인 것을 이르는 말입니다. 여기서 a의 부호는 양수든 음수든 0이든 상관없습니다. 몇가지 예를 들어보겠습니다.

n제곱근 a, a의 n제곱근, 두 말뜻이 헷갈리는 학생이 있을줄로 압니다. 본문의 흐름대로 n제곱근 a는, a의 n제곱근 중에서 실수인 것을 찾는 과정속에서 등장하는 하나의 약속이라고 이해하면 됩니다.
ii) n이 짝수일 때
n이 짝수일 때 y=xⁿ은 우함수가 되고 따라서 y축 대칭인 함수가 됩니다. 이 때 함수는 원점 (0, 0)과 두 정점 (1, 1), (-1, 1)을 항상 지난다는 특징이 있습니다.
ⓐ a가 양수일 때
n이 짝수이고 a가 양수이면, 좌표평면상에서 두 함수 y=xⁿ과 y=a는 아래 그림과 같이 나타납니다.

교점이 두 개 존재하므로 이 경우에 a의 n제곱근중 실수인 것은 두 개가 됩니다. 이 중 양수인 것을 ⁿ√a 로 표기하기로 약속한다면, 4사분면쪽의 교점의 x좌표는 대칭성에 의해 -ⁿ√a 라는 걸 확인할 수 있습니다.
ⓑ a가 0일 때
이 경우 좌표평면 상에서 그림은 아래와 같이 나타납니다.

교점의 개수는 하나이며, 교점은 원점 O(0, 0)으로 주어집니다. 따라서 n이 짝수일 때 0의 n제곱근 중 실수인 것은 홀수일때와 마찬가지로 0이 됩니다. 이로부터 일반적인 n에 대하여 0의 n제곱근 중 실수인 것은 0이라는 걸 알 수 있습니다.

ⓒ a가 음수일 때
a가 음수일 때 두 그래프를 그려보면 아래와 같습니다.

이 경우는 교점이 존재하지 않습니다. 따라서 이로부터 n이 짝수이고 a가 음수인 경우, a의 n제곱근 중 실수인 것은 존재하지 않는다는 사실을 알 수 있습니다.
ⓓ n제곱근 a
n이 짝수인 경우 위 ⓐ,ⓑ,ⓒ 세 경우에서 살펴봤듯이 a의 n제곱근 중 실수인 것의 개수는 a의 부호에 따라 달라진다는 걸 확인할 수 있었습니다. 다시 한 번 정리하면, a가 양수인 경우 교점이 두 개, 0인 경우 한 개, 음수인 경우 교점이 하나도 없었습니다. 한편 ⓐ(a가 양수인 경우)에서 두 교점의 x좌표 중 양수인 것을 ⁿ√a로 표기하기로 약속하고, 음수인 것을 -ⁿ√a 로 뒀습니다.
따라서 n이 짝수인 경우 n제곱근 a라는 것을 정의할 때, a가 양수인 경우에만 정의할 수 있으며, 이는 "a의 n제곱근 중 실수인 것 중 양수인 것"으로 해석할 수 있습니다.

n이 홀수일 때의 정의와 약간 다르다는 것을 유념하세요. n제곱근 a는 단순히 a의 n제곱근 중 실수인 것이 아닙니다. 이는 n이 짝수일 때와 홀수일 때에 따라 달리 정의되어야 하며, 특히 짝수일 때는 a의 범위가 중요한 인자로 작용합니다. 따라서 n제곱근 a는, n이 홀수일 때엔 a의 범위에 관계없이 a의 n제곱근중 실수인 것으로, n이 짝수일 때엔 a>0일 때 a의 n제곱근 중 실수인 것 중 양수인 것에 한정하여 정의됩니다. 짝수일 때의 몇가지 예를 드는 것으로 마무리하겠습니다.

정리
이번 포스팅에서는 거듭제곱근에 대해 다뤘습니다. 가장 기본 개념인 a의 n제곱근을 소개했으며, 이로부터 a의 n제곱근 중 실수인 것을 찾는 과정에서 n제곱근 a라는 것을 약속했습니다. n제곱근 a는 a의 n제곱근 중 실수를 찾는 과정이라는 큰 맥락에서 생각하는 게 가장 빠르고 정확한 이해라 할 수 있습니다.
지금껏 정리한 것을 표로 작성해보면 아래와 같습니다.

유비무환 무비유환이라는 말이 있습니다. 잘 다루지 않는 내용이라해서 그게 중요하지 않은 건 결코 아니며, 이를 소홀히하였다간 언젠가는 화를 당할 수도 있습니다. 오히려 이런 기본적인 개념부터 시작하여 기초를 다져나가는 게 바람직한 학습 순서라고 확신합니다.
이 글로 인해 거듭제곱근을 이해하는 데 어려움을 겪던 학생들이 정확히 개념을 잡고 수능을 준비할 수 있었으면 좋겠습니다.
'고등수학' 카테고리의 다른 글
| 적분이 넓이가 되는 이유(정적분, 부정적분, 원시함수와 그래프 넓이의 관계) (3) | 2021.02.28 |
|---|---|
| 지수의 밑변환 공식, 로그의 밑변환 공식 - 개념, 유도, 적용 (0) | 2021.02.28 |
| 기수법 개요 (n진법의 이해) (0) | 2021.02.28 |
| (수열) 기본 점화식 5번 유형 - 알파값의 유도 (a=q/(p-1)) (0) | 2021.02.28 |
| (수열)군수열 개요 (0) | 2021.02.28 |




