고정 헤더 영역
상세 컨텐츠
본문
(행렬) 역행렬의 유일성과 그 응용
1. 역행렬의 유일성
고등학교 수학1에서는 역행렬을 다음과 같이 정의합니다.
「n차 정사각행렬 A와 E에 대하여 AX=XA=E인 X가 존재하면 X를 A의 역행렬이라 한다.」
이 때 X=A^{-1}로 나타내며, 특히 n=2인 경우, 즉 2차정사각행렬의 경우 행렬 A와 역행렬 A^{-1}은 아래의 관계가 있습니다.

그런데 역행렬의 유일성에 관한 내용은 좀처럼 다루지 않거나 간략히 설명하고 넘어가는데요. 이와 관련한 개념과 응용이 중요하게 적용될 때가 있습니다. 결론부터 말하면, n차 정사각행렬 A의 역행렬이 존재하면 그 역행렬은 유일합니다. 즉,
「(n차 정사각행렬에 대해) AX=E이면 XA=E이다.」
가 성립하는 것입니다. 왜냐하면 AX=E가 되는 X는 A의 역행렬로 오직 하나만 존재하며, 정의상 A 역시 X의 역행렬로 볼 수 있으므로, 순서를 바꿔서 연산한 XA의 결과 역시 단위행렬 E로 나와야 합니다.
2. 증명
역행렬의 유일성에 관한 위 증명은 고교수학 범위를 넘어섭니다. 관련 개념은 선형대수학에서 나오는데요. 요는 선형사상과 행렬은 서로 '동일(isomorphic)'하며, 선형사상의 역 사상들은 전단사(bijective)이므로 역 사상에 해당하는 역행렬 역시 교환법칙이 성립한다는 것입니다. 즉 f*g=I 이면 g*f=I인데, 이는 행렬에서 AX=E이면 XA=E 라는 것과 같은 개념입니다.
여기서는 구구절절하게 선형대수학을 논하지 않고, 다소 직관적인(하지만 적확한 증명은 아닌) 증명을 소개하겠습니다.
LA=E, AR=E인 행렬 L과 R을 생각해봅시다. (L=left, R=right)
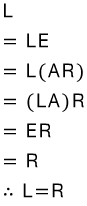
(위 전개과정에서 세 번째 등호는 행렬의 곱셈의 결합법칙이 성립함을 의미합니다.)
다시 한 번 말씀드리지만, 위 증명은 정확한 증명은 아닙니다. 「LA=E이고 AR=E이면 L=R이다」를 증명했다고 해서 「XA=E이면 AX=E이다」를 온전히 증명한 것은 아니기 때문입니다. 다만 여러분의 이해를 돕기 위해 비슷한 증명을 해보인 것에 지나지 않습니다. 더 심도깊은 내용은 대학교 선형대수학 강의에서 배우시기 바랍니다.
3. 적용
역행렬의 유일성에 관한 내용을 알아야 풀 수 있는 문제가 있습니다.
i) A+AB=E, AB+BA=A+B일 때 B의 역행렬은?
(풀이) 먼저 첫번째 조건에서 역행렬 관계를 찾을 수 있습니다.

즉 두 행렬 A, E+B는 서로 역행렬 관계이며, 이들은 역행렬의 유일성에 의해 교환법칙이 성립합니다.

두 식을 풀어보면 다음 결과를 얻습니다.

공교롭게도 두 행렬 A, B 사이에도 곱셈의 교환법칙이 성립하는군요. 이제 이를 문제의 두번째 조건에 대입합시다.

여기에 첫번째 조건(A+AB=E)을 대입하면,

따라서 B의 역행렬은 3A-E(답)로 나옵니다. 위에서 역행렬의 유일성 「AX=E이면 XA=E이다.」를 적용하여 궁극적으로 우리가 원하는 AB=BA라는 결과를 얻는 과정에 주목하시기 바랍니다. //끝
ii) ABC=E, ACB=E 일 때 AⁿBⁿCⁿ은?
(풀이) 두 조건에서 역행렬의 관계를 다음과 같이 이끌어낼 수 있습니다. (결합법칙)
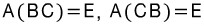
즉 A의 역행렬은 BC이면서 CB인데, 이 두 행렬이 같아야 합니다. (역행렬의 유일성)

한편, 첫번째 조건에서 (역행렬이 유일하기때문에) 이들간의 교환법칙이 성립합니다.

결합법칙을 적용하면,

B의 역행렬이 CA임을 알 수 있습니다. 한편, 두번째 조건에서도 B의 역행렬을 구할 수 있습니다.

같은 논리로 CA와 AC가 B의 역행렬로 서로 같아야 합니다.

한편,두번째 조건에서 (역행렬이 유일하기 때문에) 이들간의 교환법칙이 성립합니다.

다시 결합법칙을 적용하면,

C의 역행렬이 BA임을 알 수 있습니다. 한편, 첫번째 조건에서도 C의 역행렬을 구할 수 있습니다.

마찬가지로 AB와 BA가 C의 역행렬로 서로 같아야 합니다.

(1), (2), (3)에 의해 A, B, C중 각각의 두 행렬끼리 서로 교환법칙이 성립함을 알 수 있습니다. 이제 이로부터 AⁿBⁿCⁿ을 구해봅시다. 그에앞서 A²B²C²을 먼저 구해보면,

각 과정에서 행렬의 결합법칙과, 위에서 유도한 교환법칙을 엄밀하게 적용한 방법에 주목하세요. 이런 식으로 하면 AⁿBⁿCⁿ도 마찬가지로 (ABC)ⁿ 꼴로 묶을 수 있습니다. (AⁿBⁿCⁿ은 왼쪽에는 A가, 가운데에는 B가, 오른쪽에는 C가 n개씩 서로 몰려있는 꼴인데 앞의 방식처럼 하면 A, B, C간에 서로 이동을 할 수 있어서 (ABC)(ABC)...(ABC)의 꼴로 만들어 낼 수 있습니다.) 따라서 첫번째 조건에서 ABC=E 이므로, 식을 정리한 결과는 Eⁿ이 되어 답은 단위행렬 E가 됩니다. //끝
행렬의 진위 판별 문제는 학생들이 많이 어려워하는 부분입니다. 이 부분에서는 행렬의 특징을 제대로 파악해서 엄밀하게 '내가 아는 것'을 적용하는 연습이 필요합니다.
이번 포스팅에서는 역행렬의 유일성에 대한 중요성을 짚고, 이를 실제 문제에 적용해보았습니다. 역행렬의 개념과 곱셈의 결합법칙, 교환법칙을 제대로 아는 게 중요하며, 특히 행렬의 진위를 판별하는 문제를 해결하기 위해선 하나라도 미심쩍은 부분이 있으면 다시 한 번 사고하고 정리하는 습관이 필요합니다.
제 글이 많은 학생들에게 도움이 됐으면 합니다.
'고등수학' 카테고리의 다른 글
| (수열) 기본 점화식 5번 유형 - 알파값의 유도 (a=q/(p-1)) (0) | 2021.02.28 |
|---|---|
| (수열)군수열 개요 (0) | 2021.02.28 |
| 자연수의 거듭 제곱의 합 (시그마 공식 유도) (0) | 2021.02.28 |
| (수열)계차수열의 직관적 이해 (0) | 2021.02.28 |
| 부분분수의 변형 - 두 개짜리, 세 개짜리 (0) | 2021.02.28 |




