고정 헤더 영역
상세 컨텐츠
본문
자연수의 거듭 제곱의 합 (시그마 공식 유도)
- ∑k, ∑k², ∑k³, ∑k⁴
이 포스팅은 자연수의 거듭제곱의 합 공식 유도에 관한 글 입니다.
여러가지 수열에서 처음 등장하는 시그마(∑). 시그마를 잘 다루기 위해서는 관련 공식을 이해하고 적용하는 게 중요한데요. 그 중 자연수의 거듭제곱의 합에 관한 공식이 많이 쓰이기 때문에 이를 반드시 알아둬야 합니다. 이번 포스팅에서는 자연수의 n제곱의 합의 공식을 유도하고, 그 방법론을 제시하고자 합니다.
이 글이 필요한 학생은
1. 자연수의 거듭제곱의 합 공식이 궁금한 학생
2. 시그마(sigma)관련 공식 유도가 궁금한 학생
3. 자연수의 제곱, 세제곱, 네제곱 등의 합이 궁금한 학생
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
자연수의 거듭제곱 꼴의 합 공식
1. 시그마(sigma, ∑)의 도입
수열의 합을 구할 때 시그마라는 기호를 도입해서 다음과 같이 나타냅니다.

위 식의 의미는 k에 1, 2, 3,...을 각각 대입하면서 각 항을 더하되, n항까지 더하라는 뜻입니다.
2. 자연수의 거듭제곱 꼴의 합 공식(ak = k, k 제곱, k 세제곱, k 네제곱, ...)
위 식에서 ak가 k에 관한 다항식으로 주어지는 경우가 많습니다. 보통 k의 제곱의 합까지 많이 나오나, 세제곱도 간혹 등장합니다.
i) ak = k (자연수 n개의 합, sigma k)
n개의 자연수의 합, 1+2+3+...+n 은 다음과 같이 주어집니다.

이 수열의 합은 첫째항이 1, 공차가 1인 등차수열의 합으로 수학자 가우스가 10살 때 이미 얻어낸 공식입니다.
ii) ak = k² (자연수의 제곱의 합, sigma k^2)
n개의 자연수의 제곱의 합 1²+2²+3²+....n² 은 다음과 같이 주어집니다.

iii) ak = k³ (자연수의 세제곱의 합, sigma k^3)
n개의 자연수의 세제곱의 합 1³+2³+3³+....n³ 은 다음과 같이 주어집니다.

iv) ak = k⁴(자연수의 네제곱의 합, sigma k^4)
n개의 자연수의 네제곱의 합 1⁴+2⁴+3ⁿ+....n⁴ 은 다음과 같이 주어집니다.

시그마 공식 증명
1. sigma k (k=1 to n)
이 공식은 등차수열의 합 공식을 유도할 때와 같은 원리로 유도할 수 있습니다. 수학자 가우스는 다음 자연수의 합 S = 1+2+3+ ... +n 을 순서를 뒤집어서 계산하는 아이디어를 제시했습니다.

식의 양 변을 더하면 좌변은 2S가 되고, 우변의 각 항들을 더하면 (n+1)이 나옵니다.

즉, (n+1)이 n개가 있는 상황이 발생합니다. 식을 정리하면 다음 공식을 얻을 수 있습니다.

유도완료//
2. sigma k^2 (k=1 to n)
자연수의 제곱의 합은 (x+1)³의 전개식(곱셈공식)을 이용합니다.

이제부터 위 식의 x에 각각 1, 2, 3, .... n 까지 대입할 것입니다.(아래)

식 전체를 더하면 좌변에서 1³과 (n+1)³을 제외한 나머지 항들은 서로 상쇄되어 최종적으로 (n+1)³-1³이 남고, 우변에서는 3k² 꼴, 3k꼴, 1이 각각 n개씩 더해집니다.
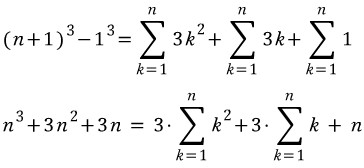
위 식의 우변의 두번째 항(sigma k)은 앞에서 n(n+1)/2로 구했으므로 이를 대입해서 식을 정리하면,

유도완료// (편의상 간단한 계산은 건너뛰었습니다.)
3. sigma k^3 (k=1 to n)
자연수의 세제곱의 합은 (x+1)⁴의 전개식(곱셈공식)을 이용합니다. (네제곱, 다섯제곱, 여섯제곱, ...등의 고차 거듭제곱의 합도 같은 방법으로 하면 됩니다.)
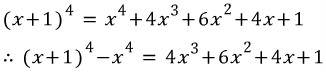
이제부터 위 식의 x에 각각 1, 2, 3, .... n 까지 대입할 것입니다.(아래)

식 전체를 더하면 좌변에서 1⁴과 (n+1)⁴을 제외한 나머지 항들은 서로 상쇄되어 최종적으로 (n+1)⁴-1⁴이 남고, 우변에서는 4k³꼴, 6k² 꼴, 4k꼴, 1이 각각 n개씩 더해집니다.

위 식의 우변의 두번째, 세번째 항(sigma k, k²)은 앞에서 구했으므로 이를 대입해서 식을 정리하면,

유도완료// (편의상 간단한 계산은 건너뛰었습니다.)
3. sigma k^4 (k=1 to n)
위와 같은 논리로, 자연수의 네제곱의 합은 (x+1)^5의 전개식(곱셈공식)을 이용합니다.

이제부터 위 식의 x에 각각 1, 2, 3, .... n 까지 대입할 것입니다.(아래)

식 전체를 더하면 좌변에서 1^5과 (n+1)^5을 제외한 나머지 항들은 서로 상쇄되어 최종적으로 (n+1)^5-1^5이 남고, 우변에서는 5k⁴꼴, 10k³꼴, 10k² 꼴, 5k꼴, 1이 각각 n개씩 더해집니다.

위 식의 우변의 두번째, 세번째, 네번째 항(sigma k, k², k³)은 앞에서 구했으므로 이를 대입해서 식을 정리하면,

유도완료// (편의상 간단한 계산은 건너뛰었습니다.)
5. 기타(sigma k^5, k^6)
나머지 자연수의 고차 거듭 제곱의 합 공식을 소개하겠습니다. (sigma k^5, k^6)

증명은 위와 비슷한 방식으로 접근하면 됩니다.
이번 포스팅에서는
1. n개의 자연수의 합 공식과 그 유도
2. n개의 자연수의 제곱, 세제곱, 네제곱의 합 공식과 그 유도
3. 자연수의 거듭 제곱의 합공식을 유도하는 방법론
에 대해서 알아보았습니다.
위 공식들이 어떤 식으로 유도됐는 지, 그 아이디어를 소개하고자 이 글을 썼습니다.
특히 (x+1)ⁿ-xⁿ으로부터 어떻게 '합공식'이 나오는 지는 눈여겨볼 만합니다.
한편, 시그마 관련 공식은 수능을 준비하는 학생이라면 능숙하게 다룰 줄 알아야 합니다. 공식유도뿐만 아니라 식을 외워서 적재적소에 활용할 수 있도록 연습하는 게 중요합니다.
제 글이 많은 학생들에게 도움이 됐으면 좋겠습니다.
'고등수학' 카테고리의 다른 글
| (수열)군수열 개요 (0) | 2021.02.28 |
|---|---|
| (행렬) 역행렬의 유일성과 그 응용 (0) | 2021.02.28 |
| (수열)계차수열의 직관적 이해 (0) | 2021.02.28 |
| 부분분수의 변형 - 두 개짜리, 세 개짜리 (0) | 2021.02.28 |
| 무한급수 ∑1/n 의 발산 증명 (0) | 2021.02.28 |




