고정 헤더 영역
상세 컨텐츠
본문
::벡터의 내적과 삼각형의 넓이 공식::
삼각형의 넓이를 구하는 방법에는 여러가지가 있으나, 벡터의 내적을 이용한 아래 공식도 있습니다.

즉, 두 벡터의 크기와 내적에 관한 정보만 있으면 두 벡터에 의해 만들어지는 삼각형의 넓이를 구할 수 있습니다. 이제부터는 이에 관한 공식 유도 과정을 알아보겠습니다.
<벡터의 내적과 삼각형의 넓이 공식 유도>

위 그림과같이 두 벡터 a, b가 각도 θ를 이루고 있고, 그로 인해 만들어지는 가상의 삼각형 AOB를 생각해봅시다. 그러면 삼각형 AOB의 넓이는 아래와 같이 주어집니다.
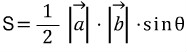
(두 변과 그 끼인각이 주어졌을 때 삼각형의 넓이는 각 변과 끼인각의 사인값을 곱해서 2로 나누어주면 구할 수 있습니다. 관련 내용은 다음 링크에 정리되어있습니다.)
https://color-change.tistory.com/4
이제 문제는 두 벡터가 이루는 각의 사인값을 구하는 것으로 귀결되는데요. 이를 위해서는 다음 내적의 정의를 이용하면 됩니다.

이제 다음 삼각비의 제곱공식을 통해 코사인값을 사인값과 연결시켜주면 됩니다.
(어떤 각의 코사인값을 안다는 것은 사인값, 탄젠트값 등의 모든 삼각비를 구할 수 있다는 말입니다. 삼각함수란 말 그대로 어떤 각을 집어넣었을 때 하나의 삼각비 값이 나오는 관계인데, 즉 한 각이 주어지면 그로부터 결정되는 모든 삼각비들이 오직 하나의 값으로 정해집니다. 삼각비에 관한 제곱공식이나 탄젠트를 사인과 코사인으로 표현하는 공식등이 이들 관계를 연결해주는 것이죠.)

이 결과를 삼각형의 넓이를 구하는 원래의 식에 대입하되, 넓이는 양수값을 가져야하므로 양의 부호만 살려서 대입, 정리하면 다음 결과를 얻습니다.

두 벡터의 크기와 그들의 내적만 주어지면 위 공식에 의해 삼각형의 넓이를 구할 수 있습니다. //끝
'고등수학' 카테고리의 다른 글
| 구의 부피 구하는 방법 - 구의 부피 공식 유도 (8) | 2021.06.20 |
|---|---|
| 해와 근의 차이점 (0) | 2021.06.20 |
| (기하와 벡터) 회전변환 식 유도 (1) | 2021.06.19 |
| 타원의 넓이 구하기(치환적분) (4) | 2021.06.19 |
| 정사영의 정의/공식/고난이도 문제 (0) | 2021.06.19 |




