고정 헤더 영역
상세 컨텐츠
본문
(총정리) 삼각형의 넓이 구하는 공식
이 포스팅은
삼각형의 넓이를 구하는 공식과 그 유도과정을
초,중,고 모든 학생을 망라하여 총정리한 글 입니다.
현업에서 수학을 많이 쓰는 사람으로서,
그간 제가 해오던 방식대로 수학적 사고 과정을 고스란히 담아내면
많은 학생들에게 도움이 되지 않을까하여 이렇게 글을 씁니다.
이 글이 필요한 학생은
1. 삼각형의 넓이를 구하는 여러 방법을 알고싶은 학생
2. 도형에 대한 감이 없는 학생
3. 도형에 대한 자신이 없는 학생
입니다.
2. 삼각형의 넓이구하는 공식
삼각형의 넓이 구하는 공식 정리: 총 6가지 공식
삼각형 넓이 구하는 공식은 총 여섯가지로 요약할 수 있습니다.






특히 공식 3)을 헤론의 공식이라 부릅니다.
위 공식에서 쓰인 여러 문자의 의미는 다음과 같습니다
S : 삼각형의 넓이
a, b, c : 삼각형의 세 변의 길이
h : 삼각형의 높이
θ : 삼각형에서 두 변의 끼인각
x₁,x₂,x₃,y₁,y₂,y₃ : 좌표평면에서 삼각형을 이루는 세 점의 좌표.
R : 삼각형의 외접원의 반지름
r : 삼각형의 내접원의 반지름
삼각형 넓이 공식 유도
1)삼각형의 넓이의 정의
식 1)은 초등학교 때 배운 삼각형의 넓의의 정의입니다. 따라서 따로 유도할 게 없습니다.
(엄밀히 말하면 사각형 넓이의 정의에서 파생되어 나온 것입니다.)

위와 같은 삼각형의 넓이는 밑변과 높이의 곱을 반으로 나눈 것 입니다. (정의)

2) 두 변과 그 끼인각을 이용한 넓이 계산
공식 2)는 1)을 제외한 나머지 식들 중 가장 근간이 되는 식 입니다.
나머지 식은 모두 이 식으로부터 나오므로 반드시 이해하시기 바랍니다.
공식 유도는 그리 어렵지 않습니다.
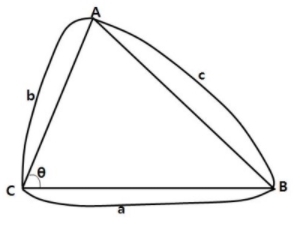
아래 그림과 같이, 삼각형의 두 변과 그 끼인각이 주어진 상황이 있습니다.

위 그림에서 삼각형의 밑변을 a로 보고, 그 때의 높이를 b와 θ로 표현하면,
아래 그림처럼 높이= bsinθ가 됩니다.

삼각형의 넓이의 정의 「밑변 곱하기 높이 나누기 2」를 적용하면
삼각형의 두 변 a, b와 그 끼인각 θ가 주어진 경우의 넓이 공식이 유도됩니다.

3) 세 변이 주어진 경우의 넓이(헤론의 공식 유도)
삼각형의 세 변이 주어진 경우 넓이 구하는 공식이 있습니다.
헤론에 의해 유도되었다해서 헤론의 공식으로 알려져 있는데요.
이제부터 헤론의 공식 유도를 하겠습니다.
단, 헤론의 공식은 외우지 마시고 유도과정과 아이디어만 잘 이해하시기 바랍니다.
아이디어는 간단합니다.
세 변으로부터 아무 끼인각 하나를 구해 공식 2)에 대입 하면 됩니다.
삼각형의 세 변이 주어졌을 때 한 각도를 구하는 방법으로는 코사인 제 2법칙 이 있습니다.
삼각형의 세 변이 주어진 아래 그림에서 (θ는 현재 모르는 값입니다.)

코사인 제 2법칙을 이용해 cosθ를 구하면

그런데 우리가 필요한 건 공식 2)에 대입할 수 있는 sinθ 입니다.
세 종류의 삼각비(sin, cos, tan) 중 하나만 주어지면 나머지 두 개는 자동적으로 구할 수 있습니다.
이와 관련된 공식이 아래 두 공식인데요,


우리는 위의 두 식 중 첫번째 식(제곱공식이라 불림)을 이용해 sinθ를 구해보겠습니다.

이를 공식 2)에 대입하면,

사실 여기까지만 해도 됩니다.
식을 보면 삼각형의 넓이가 세 변의 길이 a, b, c 만으로 나타내졌음을 알 수 있으니까요.
헤론은 이를 좀 더 기억하기 쉽게 하기 위해 임의의 매개변수 s를 도입 한 것 뿐입니다.

라 두면, 위 식은 아래와 같이 멋지게 바뀝니다.
(궁금하시면 직접 s를 대입해서 비교해보시길 바랍니다.)

4) 삼각형의 외접원의 반지름과 세 변이 주어졌을 때

위 그림에서 다음 식이 성립합니다.

이를 사인법칙 이라고 부릅니다.
사인법칙에서 sinC를 c와 R로 표현하면 다음과 같이 됩니다.

이제 이 식을 넓이 공식 2)에 대입할텐데요.
공식 2)에서 주어진 두 변을 a와 b라 보면 그 때의 끼인각은 위 그림에서 각C에 대응합니다. 따라서,


5) 삼각형의 내접원의 반지름과 세 변이 주어졌을 때

위 그림에서 분할된 세 삼각형의 넓이는



와 같습니다. 이들 세 넓이의 합이 전체 삼각형 넓이 S와 같으므로,

6) 삼각형의 세 꼭지점의 좌표가 주어졌을 때
i) 두 점으로 이뤄진 선분의 길이를 구합니다. 이 선분을 삼각형의 밑변으로 봅니다.
ii) 그 두 점을 지나는 직선의 방정식을 구하고,
ii) 그 직선과 나머지 한 점 사이의 거리를 구합니다. 이 거리가 삼각형의 높이가 됩니다.
iii) 삼각형의 넓이의 정의 (밑변 곱하기 높이 나누기 2)에 대입하여 넓이를 구합니다.

1) 밑변의 길이
위 그림에서 점 A(x1,y1), B(x2, y2)사이의 거리는 다음과 같습니다.

2) A, B를 지나는 직선의 방정식
A, B를 지나는 직선의 방정식의 기울기는 아래와 같습니다.

직선은 점 A(x1, y1)을 지나므로 이를 고려해 직선의 방정식을 구하면 다음과 같습니다.

표준형으로 표현된 위 식을 직선의 방정식의 일반형(ax+by+c=0꼴)으로 고치면 아래와 같습니다.

3) 삼각형의 높이
한 정점과 직선사이의 거리는 아래 공식을 이용해 구할 수 있습니다.

이를 이용해 점 C(x3, y3)와, 2)에서 구한 직선의 방정식 거리(삼각형의 높이)를 구할 수 있습니다.

iv) 넓이

공식 유도 완료.
이제 이 공식을 외우는 쉬운 방법 을 알려드리겠습니다.
먼저 다음과 같이 씁니다.

절댓값 안을 채울 때 윗줄에는 차례로 x1, x2, x3을 쓰고 마지막에는 처음에 썼던 x1을 씁니다.
아랫줄도 같은 방식으로 y1, y2, y3을 쓰고 마지막에 처음에 썼던 y1을 씁니다.
그 후, 아래와 같이 화살표를 긋습니다.

먼저 x1, x2, x3 에서 오른쪽 아래로 화살표를 긋습니다. (붉은색 화살표)
그렇게 이뤄진 쌍끼리 곱해서 더합니다. (x1y2 + x2y3 + x3y1)
다음으로 끝의 x1부터 시작해서 x3, x2에서 왼쪽 아래로 화살표를 긋습니다. (파란색 화살표)
그렇게 이뤄진 쌍끼리 곱해서 더합니다. (x1y3 + x3y2 + x2y1)
위의 경우 '오른쪽'이기 때문에 + 부호를,
아래의 경우 '왼쪽'이기 때문에 - 부호를 붙여주고, 이들을 더합니다.
그러면 다음 공식이 만들어집니다.

정리
4. 정리
이번 포스팅에서는
1. 삼각형의 여러가지 공식과,
2. 공식 유도 방법
에 대해 알아보았습니다.
특히 공식 2)는 가장 기본이 되는 식이며,
이 공식으로부터 다른 여러 공식들이 유도되므로 매우 중요한 공식입니다.
헤론의 공식이라 불리는 공식 3)의 경우, 공식을 외우려 하지 마시고
세 변의 길이가 주어졌을 때 삼각형의 넓이를 구하는 과정을 이해하기 바랍니다.
i) 세 변으로부터 나머지 한 각의 코사인값을 구하고(코사인 제 2법칙)
ii) 그 코사인값으로부터 사인값을 구한 뒤(제곱공식)
iii) 공식 2)에 대입하면 됩니다.
삼각형의 넓이는 도형에서 가장 기본입니다.
따라서 위 공식 유도 과정을 반드시 이해해서
다양한 방법으로 삼각형의 넓이를 구할 줄 알아야합니다.
수학을 잘 하기 위해서는 부지런히 생각하고 이해해야 합니다.
단순히 공식만 암기해서는 응용문제를 풀 수 없기 때문에 꼭 원리를 이해하도록 노력하시기 바랍니다.
수학 성적은 시간을 들인만큼 돌아오며, 이걸 게을리하면 나중에 감당할 수 없는 빚으로 다가올 수 있습니다.
꼭 명심하시기 바랍니다.
'고등수학' 카테고리의 다른 글
| 삼각형의 무게중심에 관한 공식, 증명, 성질 (2) | 2021.02.27 |
|---|---|
| 삼각형 사인 법칙 증명 (0) | 2021.02.27 |
| 삼각형의 외심 공식, 증명, 성질 (0) | 2021.02.27 |
| 삼각형의 내심 공식, 증명, 성질 (0) | 2021.02.27 |
| 코사인 제 2법칙 증명 (1) | 2021.02.27 |




