고정 헤더 영역
상세 컨텐츠
본문
안녕하세요.
컬러체인지 입니다.
이 포스팅은 수1 이전 과목 중 가장 중요하다고 손꼽히는 코사인 제 2법칙 의 증명 및 식의 의미 이해에 관한 글입니다.
코사인 제 2법칙이란?
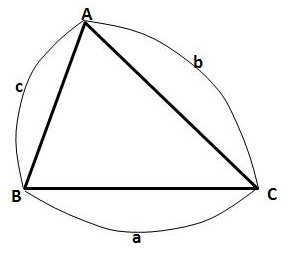
위와같은 삼각형 ABC에서,
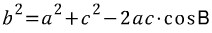
또는,
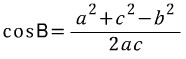
코사인 제 2법칙 증명
증명에 앞서, 짚어야 할 몇 가지가 있습니다.
첫째는 삼각형의 6요소이고,
둘째는 코사인 제1법칙 입니다.
이 두 내용을 알고 있는 학생이라면 바로 3) 코사인 제 2법칙의 증명으로 넘어가셔도 됩니다.
1. 삼각형의 6요소
삼각형이란 변 세 개와 각 세 개로 이루어 진 도형을 말합니다.
이 때, 세 개의 변과 세 개의 각을 아울러 삼각형의 6요소 라 부릅니다.
삼각형의 6요소가 중요한 이유는, 앞으로 다루게 될 모든 삼각형들의 각 요소 요소를 어떤 문자로 표현할 건 지에 관한 것이기 때문입니다.
삼각형의 6요소 중
세 개의 각은 대문자로,
세 개의 변은 소문자로
표현합니다.
이 때 중요한 규칙이 있습니다.
각 각과 마주보는 변-대변-에 같은 문자를 지정합니다.
예를들어,
각 A의 마주보는 변이 a가 되고,
각 B의 마주보는 변이 b가 되고,
각 C의 마주보는 변이 c가 됩니다.
이처럼 대변과 대각의 관계(대응하는 변과 대응하는 각의 관계)
를 가지고 삼각형의 6요소를 이해하는 게 중요합니다.
2. 코사인 제 1법칙
2) 코사인 제 1법칙
코사인 제 2법칙은 코사인 제 1법칙으로부터 유도되는 식입니다.
따라서 코사인 제 1법칙을 우선 알아야 합니다.
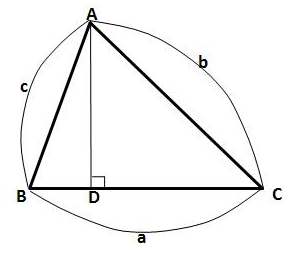
위 그림에서 꼭지점 A에서 변 a에 수선을 긋고 그 때 생기는 수선의 발을 점 D라고 하겠습니다.
이 때, 변 BD는 변 c와 각 B로 표현할 수 있습니다.
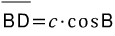
마찬가지로 변 CD는 변 b와 각 C로 표현할 수 있습니다.
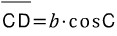
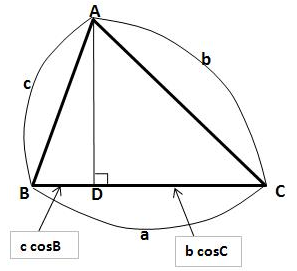
그런데 위 그림에서 변 BD와 변 CD의 합이 변 a가 되는군요.
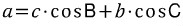
이처럼, 한 변을 나머지 두 변과 그들의 대각의 코사인값으로 표현하는 것을 코사인 제 1법칙 이라 합니다.
위의 예에서는 변 a를 나머지 변 b,c와 그들의 대각의 코사인값인 cosB와 cosC로 표현하였습니다.
나머지 변에 대해서도 똑같은 논리를 적용할 수 있습니다.
(여러분이 직접 해보시기 바랍니다.)
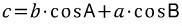
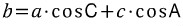
식의 패턴을 잘 파악해야 합니다.
세 식 모두 우리가 관심있어하는 특정 변이 좌변에 있고,
우변에는 그 변을 제외한 나머지 두 변과 그 변에 대응하는 대각의 코사인값이 서로 교차하며 곱해져 있습니다.
예를 들어, 마지막 식
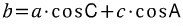
에서
관심있는 변(구하고자 하는 변) : b
나머지 두 변 : a, c
나머지 두 변의 대각의 코사인값 : cosA, cosC
서로 교차해서 곱하면 : acosC, ccosA
그들의 합 : acosC+ccosA
나머지 두 식 역시 위 '패턴'을 따르고 있습니다.
공식을 무작정 외우지 마시고 패턴을 익혀서 기억하는 걸 권장합니다.
코사인 제 2법칙
이제 본격적으로 코사인 제 2법칙을 유도하겠습니다.
이 공식 유도 과정에 녹아있는 아이디어를 잘 이해해야합니다.
수학에서 문제를 어떤 방식으로 바라보고 해결해 나가는 지가 잘 나타나기 때문입니다.
그 '방식'을 캐치하고 기억해놓는다면,
후에 또다른 문제에 그 '방식'을 적용해서 해결할 수 있을 것입니다.
각설하고,
코사인 제 2법칙은 코사인 제 1법칙으로부터 유도된다고 했습니다.
코사인 제 1법칙에 나온 식 세 개를 가져와 보면,

위와 같습니다.
우리가 목표로 하는 공식인 코사인 제 2법칙을 다시 한 번 상기하면,
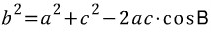
식을 잘 보면, 우리가 관심있어하는 변(b)의 제곱이 좌변에 있습니다.
우변에는 그 변을 제외한 나머지 변 두 개(a, c)가 등장하고
b의 대각 B의 코사인값이 있습니다.
코사인 제 1법칙으로부터 어떻게 제 2법칙을 유도할 수 있을까요?
바로, 코사인 제 1법칙에는 등장하지만 제 2법칙에는 등장하지 않는 군더더기 요소들을 '소거'하기만 하면 됩니다.
그러한 군더더기 요소가 cosA, cosC 임은 쉽게 파악할 수 있을 것입니다.
식(1)과 식(2)에서 cosC를 소거해보겠습니다.
식(1)에서 cosC의 계수는 b, 식(2)에서 cosC의 계수는 a입니다.
계수가 다르면 소거가 불가능하기 때문에 계수를 같게 맞춰주려면
식(1)에는 양 변에 a를 곱하고, 식(2)에는 양 변에 b를 곱해서
두 식의 계수를 ab로 맞춰주면 됩니다.
식(1)의 양 변에 a를 곱하면,
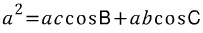
식(2)의 양 변에 b를 곱하면,
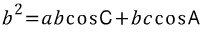
두 식을 빼면,
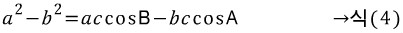
cosC가 소거됐습니다.
이제 cosA를 소거해봅시다.
마찬가지 방법으로, 식(3)과 식(4)에서 등장하는 cosA의 계수를 맞춰줍시다.
식(3)에서 cosA의 계수는 b,
식(4)에서 cosA의 계수는 -bc이므로,
식(3)에만 양 변에 c를 곱하면 될 것입니다.
식(3)의 양변에 c를 곱하면
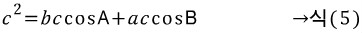
식(4)와 식(5)를 더하면
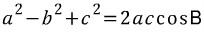
식을 b²에 관해 정리하면,
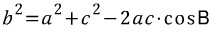
이로써 코사인 제 2법칙이 유도됐습니다.
식을 cosB에 관해서 정리하면
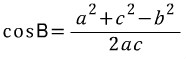
두 식 모두 코사인 제 2법칙이라 부릅니다.
코사인 제 2법칙의 의미 (중요!!!)
코사인 제 2법칙은 유도과정도 중요하지만 식의 의미를 이해하는 게 더 중요합니다. 원래 삼각형의 그림과 코사인 제 2법칙을 봅시다.
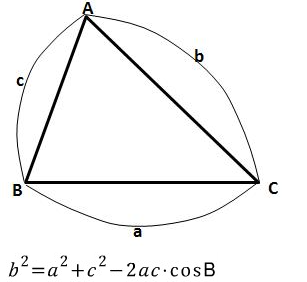
좌변은 우리가 관심있어하는(혹은 구하고자 하는) 변입니다.
우변은 그 대상을 다른 요소들로 표현한 식입니다.
그림상으로 보면,
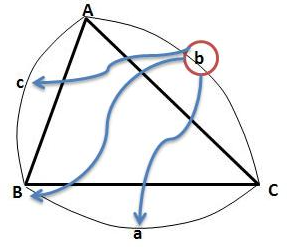
b를 구하기 위해선
a와 c, 그리고 각B (혹은 그 각의 코사인 값인 cosB)가 필요합니다.
위 삼각형의 6요소 (A,B,C, a,b,c)는 임의로 정해 진 것입니다.
따라서 이를 좀 더 일반화 시켜 말할 수도 있을 것입니다,
코사인 제 2법칙은
삼각형의 특정 변을, 나머지 두 변과 그 끼인각을 사용해서 구할 때 쓰는 공식입니다.
코사인 제 2법칙의 또다른 형태
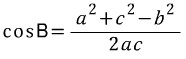
역시 비슷하게 해석될 수 있습니다.
우리가 관심있는 것은 좌변에 있는 각도 B(좀 더 엄밀히 말하면, 이 각도에 cos함수가 취해진 형태) 입니다.
우변에는 삼각형의 세 변이 모두 들어 있습니다.
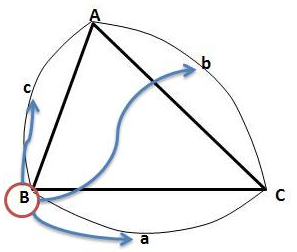
즉, 각도 B를 알아내기 위해선-비록 그 각도의 코사인값을 알아내는 간접적인 방법이긴 합니다만
나머지 세 변 a,b,c가 필요합니다.
(여기서 주목할 점은, 각 B의 대변 b는 나머지 두 변 a, c와는 다르게 분자에 자기 혼자만 부호가 반대인 채로 등장하고 있다는 것입니다.)
이를 일반화 시키면,
코사인 제 2법칙의 또다른 형태는
삼각형의 특정 각을, 나머지 세 변을 이용해서 구할 때 쓰는 공식입니다.
정리
코사인 제 2법칙은 수능과목 직전에 등장하는 공식으로, 그 중요도 및 효용성이 비수능 과목 통틀어 가장 큰 공식이라 할 수 있습니다.
이 포스팅에서는
1. 삼각형의 6요소
2. 코사인 제 1법칙
3. 코사인 제 2법칙
을 유도했습니다.
공식 유도 속에 녹아있는 아이디어였던
군더더기 요소를 소거함으로써 식에서 제외 시키는 기법에 대해 언급했으며,
코사인 제 2법칙의 의미, 식이 언제 어떤 상황에서 사용될 수 있는지에 대해서 해석해보았습니다.
'고등수학' 카테고리의 다른 글
| 삼각형의 무게중심에 관한 공식, 증명, 성질 (2) | 2021.02.27 |
|---|---|
| 삼각형 사인 법칙 증명 (0) | 2021.02.27 |
| 삼각형의 외심 공식, 증명, 성질 (0) | 2021.02.27 |
| (총정리) 삼각형의 넓이 구하는 공식 (1) | 2021.02.27 |
| 삼각형의 내심 공식, 증명, 성질 (0) | 2021.02.27 |




