고정 헤더 영역
상세 컨텐츠
본문
[총정리] 기하학적 의미를 갖는 함수 관련 수식들
1. 개념 소개
교과과정에는 소개되지 않지만 수능이나 모의고사에는 종종 등장하는 개념들이 있습니다. 그런 것들이 수험생으로하여금 수능을 어렵게 느끼게 만드는 요인인데요. 이번 포스팅에서 다룰 내용도 이에 관한 것입니다. 교과서엔 나오지 않지만 한 번 알아두면 도움이 될 것 같기에 나름대로 정리해보고자 합니다.
어떤 함수가 있으면 그 함수로 표현할 수 있는 수식중에 기하학적으로 의미가 있는 것들이 여러가지가 있습니다. 여기서 기하학적으로 의미가 있다는 얘기는, 좌표계 상에서 육안으로도 명확한 해석이 가능하다는 말입니다. 예를 들어 다음 정적분 값은 'x=a부터 x=b까지 함수가 x축과 둘러싸인 부분의 넓이'라는 기하학적인 의미를 갖는다고 할 수 있습니다.


이제 이와같은 기하학적으로 의미가 있는 함수 관련 수식들에 대해 알아봅시다.
2. 기하학적 의미를 갖는 함수 관련 수식들
어떤 수식이 평면좌표에서 기하학적으로 해석되는 상황은 크게 두 가지로 분류할 수 있습니다. 하나는 기울기이고, 또다른 하나는 넓이입니다.
1) 기울기
i. f'(a)
f'(a)는 x=a에서 접선의 기울기를 의미합니다.

ii. (f(b)-f(a))/(b-a)
아래 평균변화율은 두 점 (a, f(a)), (b, f(b))의 기울기를 의미합니다.


iii. f(a)/a
f(a)/a는 원점 O와 함수위의 한 점 (a, f(a))사이의 기울기를 의미합니다. 위 평균변화율 식에서 한 점을 원점 O(0, 0)으로 잡으면 됩니다.

한편, 그림이 아래처럼 주어졌을 때,
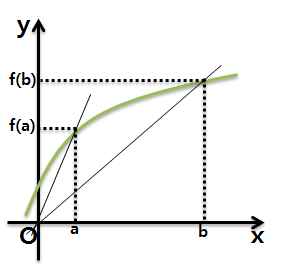
기울기를 이용하여 다음 관계를 유도할 수 있어야 합니다.

원점 O와 (a, f(a))간의 기울기가 (b, f(b))와의 기울기보다 크다는 것을 그림을 통해 알 수 있습니다. 이와 같은 해석을 기하학적 해석이라고 합니다. 그림이 저렇게 주어졌을 때 누가봐도 위 식이 성립한다는 게 명확합니다. 식이 아래와 같이 주어져도 식을 변형해서 참/거짓을 판단할 수 있어야 합니다.
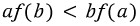
이 내용을 모르는 학생이라면 위 식이 평면상에서 어떤 의미를 지니는 지 전혀 파악하지 못할 것입니다. 식이 변형되어 나오더라도 기본을 알고 있으면 쉽게 관계를 이끌어낼 수가 있습니다.
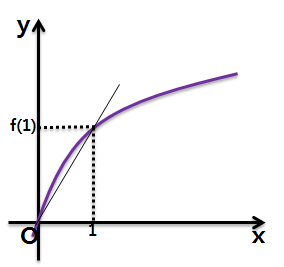
iv. f(1)
f(1)을 f(1)/1로 보면 ii와 iii에 의해 원점 O와 함수위의 한 점 (1, f(1)) 사이의 기울기로 볼 수 있습니다.
그림이 아래 처럼 주어졌을 때,

지금껏 소개한 내용을 바탕으로 다음 항들간의 대소비교를 할 줄 알아야 합니다.

그림에서 보조선이 없고 위 부등식만 주어졌다고 생각해보세요. 항들이 기하학적으로 어떤 의미를 지니는 지 모른다면 문제를 풀 수 없거나 애매하게 찍어야 하는 상황이 발생할 수 있습니다. 특히 f(1)의 경우 이를 f(1)/1로 볼 줄 아는 센스가 필요합니다.
2). 넓이
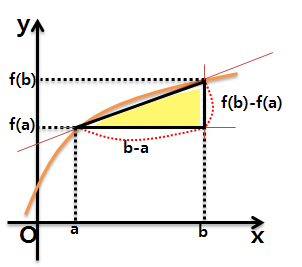
i. 1/2*(b-a)*{f(b)-f(a)}
다음 식은 좌표평면에서 삼각형의 넓이를 의미합니다.

아래 그림에서 삼각형의 밑변과 높이가 각각 (b-a), {f(b)-f(a)}로 주어지는 걸 확인할 수 있습니다.
ii. a*f(a)
a*f(a)는 원점 O와 점 (a, f(a)) 사이의 사각형 넓이를 의미합니다.

그림에서 가로와 세로가 각각 a, f(a)라는 걸 확인할 수 있습니다. 삼각형의 넓이를 나타내고싶다면 식을 1/2*a*f(a)로 변형해서 생각하면 됩니다.
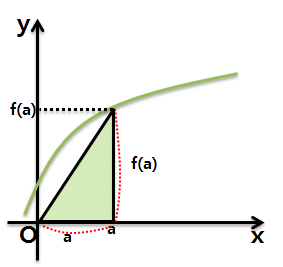
즉 다음 수식이 주어질 경우,
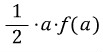
이를 '삼각형의 넓이'로 기하학적 해석을 할 줄 알아야 합니다.
iii. f(1)
f(1)을 1*f(1)로 보면, ii에 의해서 원점 O와 (1, f(1))사이의 사각형의 넓이로 해석할 수 있습니다.
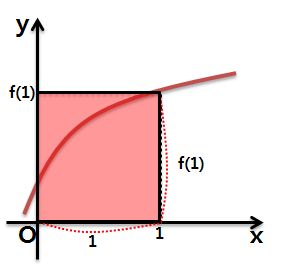
f(1)이라는 함수값은 특이하게도 기울기의 의미도 있고 넓이의 의미도 있군요. 이제부터 f(1)이라는 표현을 보는 눈이 한층 확장되었겠죠? :)
iv. f'(0)
함수 y=f(x)가 원점을 지날 때, f'(0)을 1*f'(0)으로 보면 이 값이 원점 O와 점 (1, f'(0)) 사이의 넓이라는 걸 알 수 있습니다. (아래 그림 참고)

그림에서 노란색 사각형의 넓이가 f'(0)입니다. 특히 사각형의 높이가 f'(0)이 되는 이유는 기울기의 정의로 설명할 수 있는데요. 그림에서 접선의 기울기는 f'(0)인데 이는 x가 0에서 1만큼 증가할 때 y는 0에서 f'(0)만큼 증가한다는 뜻입니다. 따라서 그림에서의 접선과 직선 x=1이 만나는 점에서 y값은 f'(0)이 되고, 따라서 사각형의 높이가 f'(0)이 되는 것입니다. 두 직선의 교점은 (1, f'(0))이 되겠군요. 중요한건 f'(0)을 위와같이 기하학적으로 해석할 줄 아는 것입니다.
v. 1/2*(b-a)*{f(a)+f(b)}
다음 식은 좌표평면에서 사다리꼴의 넓이를 의미합니다.

아래 그림에서 사다리꼴의 윗변과 밑변, 높이가 각각 f(a), f(b), (b-a)로 주어진다는 걸 확인할 수 있습니다.

vi. ∫ f(x)dx
다음 정적분값은 x=a 에서 x=b까지 함수 y=f(x)가 x축과 둘러싸인 부분의 넓이를 의미합니다.
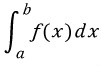
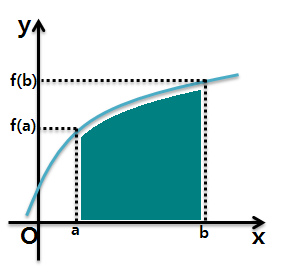
그림의 넓이는 v에서 구한 사다리꼴의 넓이보다 큰 값을 지닙니다. 이를 일반화시키면, 함수가 위로 볼록한 경우 다음 부등식이 항상 성립합니다.

함수가 아래로 오목한 형태라면 위 부등식이 반대가 되겠죠. 이는 기하학적 해석 없이는 증명이 매우 힘든 풀이입니다. 항들이 복잡하게 이항되어있다 하더라도 해석이 가능하도록 변형만시키면 그다음부터는 그림을 보고 풀어나가면 됩니다.
3. 정리
지금까지 함수 관련 여러가지 수식들의 기하학적 해석에 대해 알아봤습니다. 교과과정에서는 이 내용을 자세히 다루지 않고 있습니다. 그 이유는 함수를 아는 학생이라면 배운 내용을 토대로 식이 어떤 의미를 지니는지 추론할 수 있다고 보기 때문입니다. 따라서 이 파트는 어려운 추론문제에 종종 등장하곤 합니다.
본문에서는 다음 두 가지 사항
- 기울기
- 넓이
에 대해 어떤 수식이 어떤 의미를 지니는가를 중점적으로 살펴보았습니다. 본문엔 소개하지 않았지만 점들의 위치에 관한 기하학적 해석도 가능한 경우가 있습니다. 대표적인 예로는 내분점, 외분점, 중점등이 있습니다. 더 공부해보고싶은 학생은 고1 수학을 참고하세요.
관련 예제는 미적분과 통계기본이나 수학2에 나오는 미적분 파트에서 수능 및 평가원모의고사 기출에 많이 있습니다. 소개한 개념을 연습해보고싶은 학생은 기출문제를 참고하세요.
제 글이 많은 학생들에게 도움이 됐으면 좋겠습니다.
'고등수학' 카테고리의 다른 글
| [증명] 다항함수 x^n의 미분 (1) | 2021.03.06 |
|---|---|
| [유형별 정리]경우의 수 - 함수의 개수 문제 (0) | 2021.03.06 |
| 표본평균의 평균과 분산, 통계적 추정 - 개념, 성질, 적용 (0) | 2021.03.06 |
| 이항분포의 평균과 분산 공식 유도 (3) | 2021.03.06 |
| (총정리) 이항정리 관련 공식 유도- 개념, 응용, 공식, 증명 (3) | 2021.03.06 |




