고정 헤더 영역
상세 컨텐츠
본문
미분가능의 정의/개념/의미/적용
이 포스팅은 미분가능의 정의/개념/의미/적용에 관한 글 입니다.
미분은 고등학교를 졸업한 학생이라면 누구나 알아야 할 기본 소양입니다.
따라서 미분의 정확한 개념 및 의미를 알고 이를 자유롭게 활용할 줄 알아야 하는데요.
여기서는 미분의 정의를 간단히 짚은 뒤, 어떤 함수가 '미분 가능'하다는 게 무엇인 지 그 개념과 의미에 대해서 심도있게 다룰 것입니다.
이 글이 필요한 학생은
1. 미분의 정의가 궁금한 학생
2. 미분 가능이란 식으로 어떤 의미를 지니는 지 궁금한 학생
3. 함수의 극한, 함수의 연속, 미분계수, 도함수, 미분가능 등의 개념이 헷갈리는 학생
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
미분의 정의 및 미분 가능의 개념
모든 것은 변합니다.
한 철학자는 '변하지 않는 유일한 것은 모든 것은 변한다는 사실 뿐이다'라고 했는데요.
이처럼 어떤 양(量)의 변화율을 자연과학에서는 미분(微分)이라는 개념을 사용해 나타냅니다.
결론부터 말하자면, '미분 = 평균변화율의 극한'입니다.
평균변화율이란, 함수 y=f(x)위의 두 점 (a, f(a)), (b, f(b)) 사이에서 평균적으로 얼마만큼 함수값의 변화가 일어났는 지를 측정하는 양(量)이고,
미분이란 이 평균변화율의 구간을 최대한 잘게 쪼개서(微) 변화율을 보는, '극한'의 개념입니다.
평균변화율은 두 가지 식으로 나타낼 수 있습니다.
평균변화율의 극한으로 정의되는 미분 역시 두 가지 식으로 표현할 수 있고,
'미분 가능' 이라는 개념 역시 두 가지 식으로 표현 가능합니다.
지금부터는 이에 대해 알아보겠습니다.
- 평균변화율
구간 [a, b]에서 함수 y=f(x)의 평균변화율은 다음과 같이 주어집니다.
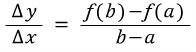
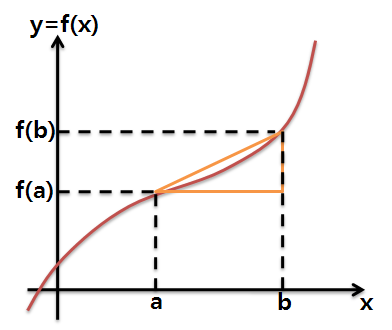
여기서 Δ(delta)는 '변화량'이라는 의미의 그리스문자입니다.
즉, x가 a에서 b만큼 변화한 그 양을 Δx (x의 증분)로, y가 f(a)에서 f(b)만큼 변화한 양을 Δy (y의 증분)로 표현하고 이들의 비를 평균변화율로 정의합니다.
한편, 위 식에서 b를 a와 Δx로 바꿔주면 평균변화율을 다른 표현으로 나타낼 수 있습니다.

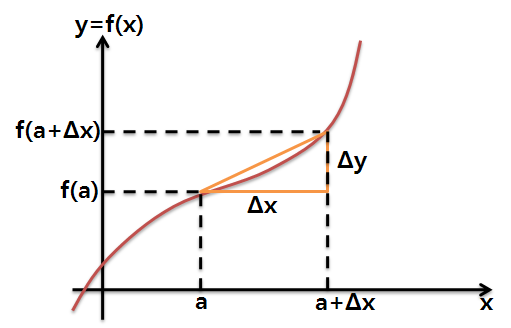
평균변화율을 위 두 가지 수식으로 표현할 줄 아는 게 중요합니다.
-미분계수
x=a 에서의 미분계수는 b가 a에 한없이 가까이 갈 때(b→a)의 평균변화율의 극한값으로 정의되고, 표기는 f'(a)로 합니다.
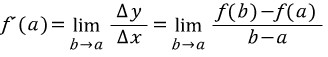
f'(a)란, x=a에서의 평균변화율의 극한값입니다. 즉, 기준점은 a이며 동점은 b입니다.
일반적으로 문자 b보다는 x가 선호되므로, 위 정의식에서 b를 x로 바꾸면 미분계수를 아래와 같이 정의할 수 있습니다.

평균변화율에서 Δx를 도입한 것처럼, 미분계수도 똑같이 Δx를 도입해서 극한을 다른 식으로 표현할 수 있습니다. b - a = Δx 에서 b가 a에 한없이 가까이 간다면, x의 증분 Δx는 0에 한없이 가까이 가겠군요.

Δx를 매번 쓰는 건 번거로우므로 이를 h로 대체합시다.


-도함수
미분계수는 특정 기준점 x=a 에서의 평균변화율의 극한값이었습니다.
그런데 매번 f'(a)의 정의를 사용하여 미분계수를 구하는 건 여간 번거로운 작업이 아닙니다.
따라서 특정점 a가 아닌 임의의 점 x에서의 미분계수를 구해놓는다면, 우리가 원하는 지점의 미분계수를 쉽게 구할 수 있을 것입니다.
임의의 점 x에서의 미분계수를 구해놓은 그 식에다가 특정 지점의 x좌표만 대입한다면(이를테면 x=a) 그에 해당하는 미분계수값(f'(a))을 바로 구할 수 있습니다.
특정 값을 넣었을 때 그에 해당하는 값(미분계수)이 하나씩 나온다, 바로 함수의 개념이죠.
도함수라 함은, 다름아닌 임의의 점 x에서의 미분계수를 구해놓은 함수식입니다.
즉, f'(a)에서의 기준점이었던 x좌표 a가 이제는 임의의 x좌표 x로 바뀐 것이며, 따라서 도함수의 표기는 f'(x)로 합니다.
우리는 위에서 정의한 f'(a)의 정의식에서 a 대신에 x로만 바꾸면 됩니다.
그런데 첫번 째 정의식(x→a, f(x)→f(a))에서 a대신 x를 넣으면 구분돼야하는 변수(동점, 기준점)가 하나의 변수 x로 표현되어버립니다.
따라서 원래의 식에서 기준점 a는 x로 치환하되, 움직이는 점 x는 t로 '표기만' 바꿔줍니다.

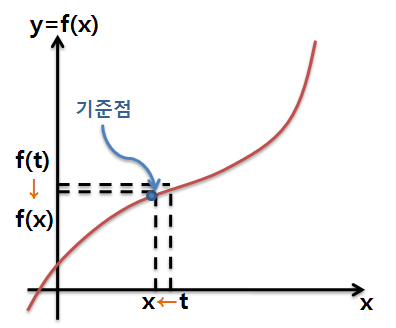
두 번째 식에서는 a를 x로만 치환해주면 됩니다.


-미분 가능
미분가능의 정의를 알아보기에 앞서 미분가능의 전제조건부터 알아봅시다.
어떤 함수가 x=a 에서 미분가능하기 위해서는, 그 지점에서 반드시 연속이어야 합니다.
(연속이 아니라면 평균변화율과 그 극한값이 있을 수 없겠죠.)
어떤 함수가 x=a 에서 미분 가능하다는 말은 무엇일까요?
바로, f'(a)를 정의했던 극한이 수렴한다는 말입니다.

식을 잘 보면, 극한(limit) 안에 있는 항들은 x에 관한 항이거나(중간식) h에 관한 항입니다.(마지막 식)
(a는 기준점으로, 미분계수를 구하고자 하는 정점입니다. 즉 식에서 a는 변하지 않습니다.)
다시말해서, 극한 속의 각각의 항들은 x 혹은 h의 함수이며 미분계수 f'(a)는 그 함수들의 극한(함수의 극한)으로 주어지고 있습니다.
f'(a)가 특정 값을 갖기 위해서는 이들 함수의 극한이 수렴해야겠죠.
정리하면, x=a 에서 미분가능하다는 말은 f'(a)가 존재한다는 의미이고,
f'(a)가 존재한다는 것은 정의된 극한식에서 함수가 수렴한다는 의미이고,
이는 다름아닌 함수의 극한이 수렴하기 위한 문제로 귀결됩니다.
함수의 극한이 수렴하려면 좌극한값과 우극한값이 동일해야합니다. (*이 값들이 함수값과 같을 필요는 없습니다. '극한값 = 함수값'은 함수의 "연속"의 필요충분조건입니다.)
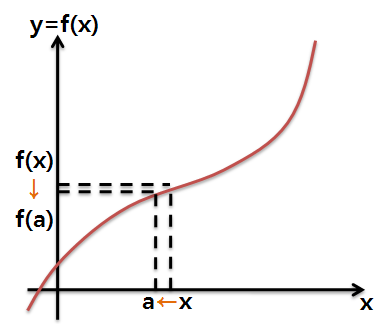
첫번 째 식부터 보겠습니다.
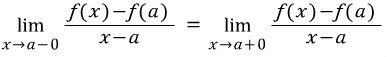
좌변은 함수 {f(x)-f(a)}/{x-a} 의 좌극한이고 우변은 이 함수의 우극한입니다.
미분에서는 이 극한들을 단순한 함수의 극한과 구분하기 위해 좌미분계수, 우미분계수 라는 용어를 씁니다.
미분가능하다는 말은 이 좌미분계수와 우미분계수 값이 같다는 말입니다.

두 번째 미분계수 표현식 역시 '좌미분계수 = 우미분계수'일 때 미분가능이라고 할 수 있습니다.
이 때 좌미분계수란, h로 표현된 x의 증분 Δx가 0보다 작은 쪽에서 0으로 가까이 가는 걸 말하고,
우미분계수란 Δx가 0보다 큰쪽으로부터 0에 한없이 가까이 가는 걸 뜻합니다.
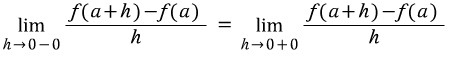
(이로 미뤄볼 때, x의 증분(增分)이라는 용어는 약간의 혼란을 야기할 수 있습니다. Δx는 꼭 양수란 법이 없기 때문입니다. 따라서 제 사견으로는 Δx를 x의 '변화량'으로 부르는 게 좀 더 정확한 표현인 것 같군요.)

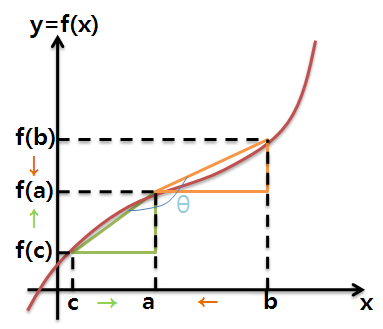
*이로써 x=a 에서의 미분계수는 (기하학적으로) 그 점에서 함수의 접선의 기울기가 되는 이유를 설명할 수 있습니다. Δx는 양에서도, 음에서도 0으로 갈 수 있습니다. 그렇게 되면 평균변화율 역시 x=a 의 좌, 우를 기준으로 설정할 수 있게 됩니다.(그림에서 주황색, 연두색 삼각형)
이렇게 x=a 의 좌, 우에서 Δx (=h) 가 0으로 갈 때의 변화양상을 잘 보면, 기울기가 점점 한 점에서의 접선의 기울기로 수렴하는 걸 알 수 있습니다. (그래프 위의 한 점에서의 접선이란, 그래프 위의 다른 점과의 각도 θ가 180˚에 가까워지는, 즉 tanθ값이 한없이 0으로 가면서 생기는 직선을 의미합니다. 그렇게 되려면 아래 그림에서 주황색, 연두색 삼각형의 평균변화율의 극한값이 같아야 하겠죠.)
미분 및 미분 가능 개념의 적용
<문제>
다음과 같이 주어진 함수 f(x)가 x=1에서 미분가능 할 때, p와 q의 값을 구하라.

<개념 적용>
i) 함수의 연속
미분가능의 전제조건은 함수의 연속이라고 했습니다.
즉 위 함수 f(x)가 x=1 에서 미분가능하려면 함수는 x=1에서 반드시 연속이어야 합니다.
「연속 : 함수의 좌극한 = 함수의 우극한 = 함수값」

각각의 구간에 대해 함수가 달리 정의되고 있으므로 좌극한에는 x<1 일때의 함수를, 우극한에는 x>1 일때의 함수를, 함수값에는 x=1 일때의 함수를 각각 적용하면 됩니다.

이들을 모두 같다고 두면 다음 관계식을 얻습니다.

(무작정 두 함수에 1을 대입해서 같다고 두지 말고, '연속'의 정확한 개념을 적용하는 습관을 기르시기 바랍니다.)
ii) 미분가능(좌미분계수, 우미분계수)
위 함수가 x=1에서 미분가능하려면 좌미분계수와 우미분계수를 같게 놓으면 됩니다.
미분가능의 두 가지 표현식 중 첫번째 식을 이용하겠습니다.

식의 좌변에서 x는 1보다 작은 구간에서 1로 접근하고, 우변에서는 1보다 큰 구간에서 1로 접근하기 때문에 식에서 f(x)는 구간별로 정의된 각각 다른 함수를 넣어 주면 됩니다.
먼저, 좌미분계수.
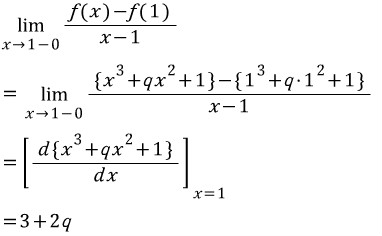
다음으로 우미분계수.

이 두 값을 같다고 두면 다음 식을 얻을 수 있습니다.

(무작정 두 함수를 미분해서 1을 대입하지 말고, 미분가능의 정확한 개념을 적용해서 문제를 푸시기 바랍니다.)
iii) 연립
i)과 ii)에서 얻은 두 식을 연립하여 답을 구할 수 있습니다.
p-q = -2
p-2q = 1
답 : p=-5 , q=-3
//끝
정리
이번 포스팅에서는
1. 평균변화율과 미분계수, 도함수의 정의.
2. 미분가능의 수학적 의미.
3. 개념의 정확한 적용.
에 대해 다뤘습니다.
미분가능은 그 특성상 정확한 개념이 정립돼있지 않은 학생에게는 매우 어려운 문제로 다가갈 수 있는 개념입니다. 출제자에겐 이보다 더 좋은 소재가 없죠.
꼬리에 꼬리를 물며 개념이 확장되는 미분파트.(평균변화율→미분계수→도함수→미분가능)
정확한 개념을 익힘으로써 아무리 어려운 문제라도 풀어낼 수 있는 내공을 쌓기 바랍니다.
제 글이 많은 학생에게 도움이 됐으면 합니다.
'고등수학' 카테고리의 다른 글
| 중복조합 - 공식 유도, 아이디어, 적용 (0) | 2021.03.06 |
|---|---|
| 원순열 - 공식 유도, 아이디어, 적용 (1) | 2021.02.28 |
| 적분이 넓이가 되는 이유(정적분, 부정적분, 원시함수와 그래프 넓이의 관계) (3) | 2021.02.28 |
| 지수의 밑변환 공식, 로그의 밑변환 공식 - 개념, 유도, 적용 (0) | 2021.02.28 |
| 거듭제곱근 개념 정리(a의 n제곱근, n제곱근 a) (1) | 2021.02.28 |




