삼각함수의 미분과 적분
::삼각함수의 미분과 적분::
이 포스팅은 삼각함수의 미분 및 적분(기본 공식 증명)에 관한 글 입니다.
삼각함수는 대표적인 초월함수로, 함수의 극한, 미분과 적분 파트에서 자주 등장합니다. 따라서 각 삼각함수별로 미분하는 법, 적분하는 법을 알아놓는게 좋습니다. 물론 지금부터 소개할 식들은 매우 기초적인 공식들입니다만, 정리 차원에서 증명까지 함께 소개하며 미적분 공식들을 정리해보겠습니다.
이 글이 필요한 학생은
1. 삼각함수의 미분에 대해 궁금한 학생
2. 삼각함수의 적분에 대해 궁금한 학생
3. 삼각함수의 미분과 적분 공식 증명이 필요한 학생
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
그럼 포스팅 시작합니다.
삼각함수의 미분과 적분
지금부터 소개할 식은 가장 기본적인 삼각함수들의 미분 및 적분에 관련된 공식들입니다. 개중에는 워낙 잘 알려져서 따로 정리할 필요가 없는 식도 있을 것이고, (특히 적분의 경우) 생각지도 못했던 식이 나올 수도 있을 것입니다. 한 번 찬찬히 살펴보시고, 이 다음에 소개할 '증명'에서 한 번 더 생각해보기 바랍니다. x의 단위는 라디안입니다.
1. 삼각함수의 미분
기본 여섯가지 삼각함수 sinx, cosx, tanx, cotx, secx, cosecx 의 미분은 다음과 같습니다.
i) y=sinx → y'=cosx
ii) y=cosx → y'=-sinx
iii) y=tanx → y'=sec²x
iv) y=cotx → y'=-cosec²x
v) y=secx → y'=secx·tanx
vi) y=cosecx → y'=-cosecx·cotx
여기서 주목할 점은, tanx와 secx가 함께 다니고 cotx와 cosecx가 함께 다닌다는 것입니다. 또한, cosx, cotx, cosecx 세 함수들(co로 시작하는 함수들)은 미분시 마이너스 부호를 달고 나오는 것도 눈여겨 볼만합니다.
2. 삼각함수의 적분
삼각함수의 적분식은 약간 까다롭습니다. 이는 직접적인 연산인 미분에 비해 적분은 태생적으로 간접적인(indirect) 연산이기 때문입니다. 적분상수는 대문자 C로 표현하였습니다.
i) y=sinx → ∫ y dx = -cosx + C
ii) y=cosx → ∫ y dx = sinx + C
iii) y=tanx → ∫ y dx = -lnlcosxl + C
iv) y=cotx → ∫ y dx = lnlsinxl + C
v) y=secx → ∫ y dx = lnlsecx+tanxl + C
vi) y=cosecx → ∫ y dx = -lnlcotx+cosecxl + C
vii) y=sec²x → ∫ y dx = tanx + C
viii) y=cosec²x → ∫ y dx = -cotx + C
ix) y=secx·tanx → ∫ y dx = secx + C
x) y=cosecx·cotx → y'= -cosecx + C
우변을 미분하면 적분하기 전의 함수(좌변)가 나옵니다.(원시함수의 개념.) 마찬가지로 tanx와 secx가 함께 다니고 cotx와 cosecx가 함께 다닙니다. 또한, v)와 vi)에서 소개한 secx와 cosecx의 적분식은 교과서에는 소개되지 않는 식들입니다. 참고로 알아놓으면 유용할 것입니다.
삼각함수의 미분과 적분 증명
1. 삼각함수의 미분
i) y=sinx → y'=cosx
삼각함수의 미분은 다음 도함수의 정의를 이용합니다.

f(x)=sinx로 보고 도함수를 구해봅시다.

두번째 등호에서 삼각함수의 덧셈공식을 이용하였고, 네번째 등호에선 삼각함수의 기본 극한 정리를 적용했습니다. (삼각함수의 기본 극한 정리가 궁금한 분은 다음 링크를 참고하세요. color-change.tistory.com/47 )
수식을 더 전개하면,

두 번째 등호에서 삼각함수의 제곱공식 (sin²x + cos²x = 1)을 이용하였고, 네 번째 등호에선 역시 삼각함수의 기본 극한 정리를 적용하였습니다. 특히 극한을 구할 때, 수렴하는 함수의 극한의 경우 사칙연산이 성립한다는 사실을 이용했습니다.
따라서 y=sinx를 미분하면 y'=cosx를 얻습니다.
ii) y=cosx → y'=-sinx
y=cosx의 미분도 같은 방법으로 증명하면 됩니다.

f(x)=cosx로 보고 도함수를 구해봅시다.
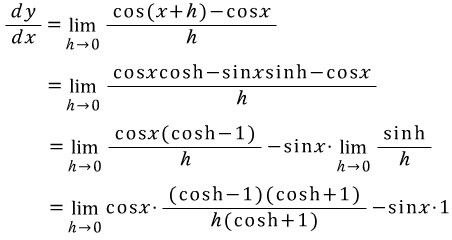
두번째 등호에서 삼각함수의 덧셈공식을 이용하였고, 네번째 등호에선 삼각함수의 기본 극한 정리를 적용했습니다. 수식을 더 전개하면,

두 번째 등호에서 삼각함수의 제곱공식 (sin²x + cos²x = 1)을 이용하였고, 네 번째 등호에선 역시 삼각함수의 기본 극한 정리를 적용하였습니다. 특히 극한을 구할 때, 수렴하는 함수의 극한의 경우 사칙연산이 성립한다는 사실을 이용했습니다.
따라서 y=cosx를 미분하면 y'=-sinx를 얻습니다.
iii) y=tanx → y'=sec²x
삼각비의 관계에 따르면 tanx = sinx / cosx 로 표현할 수 있습니다. 따라서 y=tanx의 미분은 다음 분수함수의 미분법을 이용해서 구할 수 있습니다.

y=tanx=sinx/cosx=f(x)/g(x)의 꼴로 보고 i)과 ii)에서 구한 결과를 적용하면,

제곱공식과 분수함수의 미분을 적용한 결과, y=tanx 의 도함수는 y'=sec²x 로 얻을 수 있었습니다.
iv) y=cotx → y'=-cosec²x
삼각비의 관계에 따르면 cotx = cosx / sinx 로 표현할 수 있습니다. 따라서 y=cotx의 미분은 다음 분수함수의 미분법을 이용해서 구할 수 있습니다.
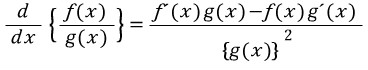
y=cotx=cosx/sinx=f(x)/g(x)의 꼴로 보고 i)과 ii)에서 구한 결과를 적용하면,

제곱공식과 분수함수의 미분을 적용한 결과, y=cotx 의 도함수는 y'=-cosec²x 로 얻을 수 있었습니다.
v) y=secx → y'=secx·tanx
삼각비의 관계에 따르면 secx=1/cosx로 표현할 수 있습니다. 따라서 y=secx의 미분은 다음 분수함수의 미분법을 이용해서 구할 수 있습니다.

y=secx=1/cosx=1/f(x)의 꼴로 보고 i)과 ii)에서 구한 결과를 적용하면,

분수함수의 미분과 삼각비의 관계를 적용한 결과, y=secx 의 도함수는 y'=secx·tanx 로 얻을 수 있었습니다.
vi) y=cosecx → y'=-cosecx·cotx
삼각비의 관계에 따르면 cosecx=1/sinx로 표현할 수 있습니다. 따라서 y=cosecx의 미분은 다음 분수함수의 미분법을 이용해서 구할 수 있습니다.

y=cosecx=1/sinx=1/f(x)의 꼴로 보고 i)과 ii)에서 구한 결과를 적용하면,
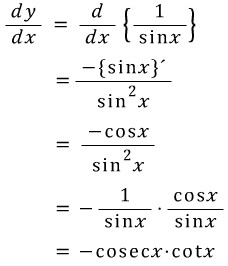
분수함수의 미분과 삼각비의 관계를 적용한 결과, y=cosecx 의 도함수는 y'=-cosecx·cotx 로 얻을 수 있었습니다.
2. 삼각함수의 적분
삼각함수의 부정적분중 몇 가지는 원시함수의 정의를 이용하면 쉽게 구할 수 있습니다.
i) y=sinx → ∫ y dx = -cosx + C
ii) y=cosx → ∫ y dx = sinx + C
iii) y=tanx → ∫ y dx = -lnlcosxl + C
iv) y=cotx → ∫ y dx = lnlsinxl + C
v) y=secx → ∫ y dx = lnlsecx+tanxl + C
vi) y=cosecx → ∫ y dx = -lnlcotx+cosecxl + C
vii) y=sec²x → ∫ y dx = tanx + C
viii) y=cosec²x → ∫ y dx = -cotx + C
ix) y=secx·tanx → ∫ y dx = secx + C
x) y=cosecx·cotx → y'= -cosecx + C
앞서 소개한 열 개의 적분식 중에서 i), ii), vii), viii), ix), x) 여섯개의 식의 우변을 미분해보면 미분법의 공식에 의해 좌변이 얻어진다는 사실을 금방 알아낼 수 있습니다. 이는 다름아닌 함수와 원시함수의 관계입니다. (물론 나머지 네 개의 식들도 우변을 미분해보면 좌변이 나옵니다.)
따라서 여기서는 나머지 네 식 iii), iv), v), vi)의 증명을 해보겠습니다.
iii) y=tanx → ∫ y dx = -lnlcosxl + C
y= tanx의 적분은 다음 분수함수의 적분법을 통해 구할 수 있습니다.

y=tanx를 sinx/cosx로 보면, 이 때 분자의 sinx가 분모의 cosx를 미분한 것과 관계가 있으므로 위 식을 적용할 수 있습니다.

이 때 절댓값을 붙여주는 이유는 로그 안의 진수는 반드시 양수여야 하기 때문입니다.
iv) y=cotx → ∫ y dx = lnlsinxl + C
y= tanx의 적분은 다음 분수함수의 적분법을 통해 구할 수 있습니다.
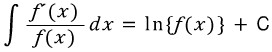
y=cotx를 cosx/sinx로 보면, 이 때 분자의 cosx가 분모의 sinx를 미분한 것과 관계가 있으므로 위 식을 적용할 수 있습니다.
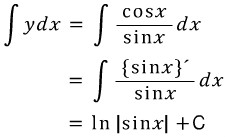
이 때 절댓값을 붙여주는 이유는 로그 안의 진수는 반드시 양수여야 하기 때문입니다.
v) y=secx → ∫ y dx = lnlsecx+tanxl + C
y=secx의 부정적분을 곧바로 구하는 방법은 없습니다. 따라서 여기선 우측의 원시함수를 미분하면 실제로 좌측의 y=secx를 얻을 수 있는 지를 확인함으로써 증명하겠습니다.
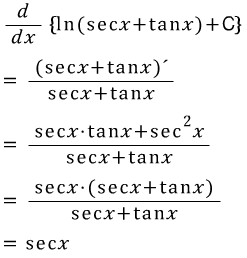
우변의 함수를 미분하면 y=secx가 나옵니다. 따라서 y=secx를 적분하면 y=lnlsecx+tanxl + C가 나옵니다. 이 때도 마찬가지로 로그 안의 진수가 양수임을 나타내기 위해 절댓값을 붙여줬습니다.
vi) y=cosecx → ∫ y dx = -lnlcotx+cosecxl + C
y=cosecx의 부정적분을 곧바로 구하는 방법은 없습니다. 따라서 여기선 우측의 원시함수를 미분하면 실제로 좌측의 y=cosecx를 얻을 수 있는 지를 확인함으로써 증명하겠습니다.

우변의 함수를 미분하면 y=cosecx가 나옵니다. 따라서 y=cosecx를 적분하면 y=-lnlcosecx+cotxl + C가 나옵니다. 이 때도 마찬가지로 로그 안의 진수가 양수임을 나타내기 위해 절댓값을 붙여줬습니다.
//끝
정리
이번 포스팅에서는
1. 삼각함수의 미분
2. 삼각함수의 적분
3. 삼각함수의 미분 공식 증명
4. 삼각함수의 적분 공식 증명
에 대해 알아보았습니다.
삼각함수의 미분과 적분은 초월함수를 다루는 자연계 고등학생이라면 반드시 알아야 할 기본중의 기본 공식입니다. 그러한 미적분 공식들이 어떻게 유도되는지, 유도과정에서 어떤 개념들이 사용되는지를 알려드리기 위하여 이 글을 썼습니다.
수많은 공식을 무조건 암기하려 하지 말고, 공식이 유도되는 과정을 잘 학습해서 자기 것으로 체화시키기 바랍니다.
제 글이 많은 학생들에게 도움이 됐으면 합니다.