구의 겉넓이 구하는 법 - 구의 겉넓이 공식 유도

구의 겉넓이 구하는 법 - 구의 겉넓이 공식 유도

 

이 포스팅은

구의 겉넓이의 공식 유도에 관한 글 입니다.

 

구의 겉넓이는 4πR²으로 그 결과만 알려줄 뿐 학교에서도, 학원에서도 증명해주지 않는

부분이라 한번 쯤은 궁금하셨을 겁니다.

그 이유는 구의 겉넓이는 대학교 때 배우는 이중적분이라는 개념을 이용해 구할 수 있기 때문입니다.

 

이 글에서는 구의 겉넓이를 구하는 데 사용되는 이중적분의 개념을 

다소 직관적이고 이해하기 쉬운 방법으로 설명하겠습니다.

글을 읽는 여러분이 고등학생이라면 그냥 가볍게 읽어보고 넘어가셔도 됩니다.

 

 

 

이 글이 필요한 학생은

1. 미분과 적분의 개념을 알고 있는 학생.

2. 구의 겉넓이를 구하는 과정을 알고 싶은 학생

3. 이중적분은 어떻게 사용되는 지 알고싶은 학생.

 

입니다.

제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.

그럼 포스팅 시작합니다.

---

 

구의 겉넓이         

 

구(sphere)란 공간좌표계의 한 정점으로부터 같은 거리에 있는 점들의 집합입니다.

(*평면좌표계의 한 정점으로부터 같은 거리에 있는 점들의 집합은 원(circle)입니다.)

 

구의 반지름을 R이라고 할 때, 겉넓이 S는 4πR² 으로 주어집니다.

 

 

---

 

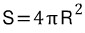
공식 유도  

 

구의 겉넓이를 구하기 위해서는 미분과 적분의 개념을 알고있어야 합니다.

미분은 어떤 요소를 한없이 작게 쪼개는 과정이고,

적분은 쪼개어진 요소 요소를 모으는 과정입니다.

 

i) 구의 표면의 미소입자를 미소단위로 표현하기.

- 구형좌표계를 도입해서 미소입자를 나타내기

이제 우리는 구를 한없이 잘게 쪼개어 작은 입자들을 만들것입니다.(미분)

 

   

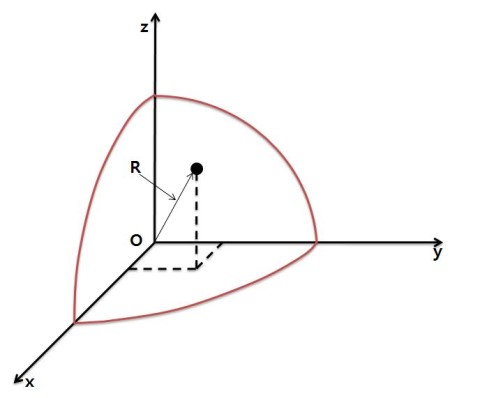
x, y, z축으로 이뤄진 공간좌표계(이를 데카르트 좌표계라 합니다.)에

중심이 원점, 반지름이 R인 구를 생각해봅시다.

편의상 그 구의 1/8과 구 위의 한 점을 그림으로 나타내면 아래와 같습니다.

 

 

 

 

좌표계에는 구형좌표계(spherical coordinate)라는 또다른 좌표계가 있습니다.

지금부터는 이를 도입하겠습니다.

 

위 그림에 나타난 구 위의 한 점에 대해서

점의 xy평면 위로의 정사영이 x축과 양의 방향으로 이루어 진 각의 크기를 θ,

화살표로 표현된 점의 위치벡터를 r축이라 하고, 

z축으로부터 r축까지의 각도를 Φ(Phi)라고 해봅시다.

 

구형좌표계의 각 요소를 그림으로 표현하면 아래와 같이 됩니다.

 

 

 

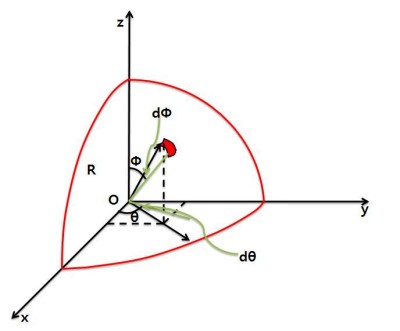
구 위의 점에서 θ, Φ방향으로 매우 작은 각도만큼 선을 그어 보겠습니다.

그 각도를 dθ, dΦ 라 합시다.

(이처럼 수학에서 매우 작은 요소를 표현할때는 소문자 d를 이용합니다.

d는 differentiation(미분)의 d로, f'(x)를 dy/dx로 표현할 때 쓰는 그 d 입니다.)

 

 

이를 그림으로 표현하면 아래와 같습니다.

 

 

 

 

- 미소입자의 넓이 구하기

이제 구를 매우 잘게 쪼갰습니다. 위 그림에 나타난 붉은색 도형이 바로 구를 한없이 잘개 쪼갰을 때 생기는 미소입자입니다.

이 도형을 확대해보면 다음과 같습니다.

 

 

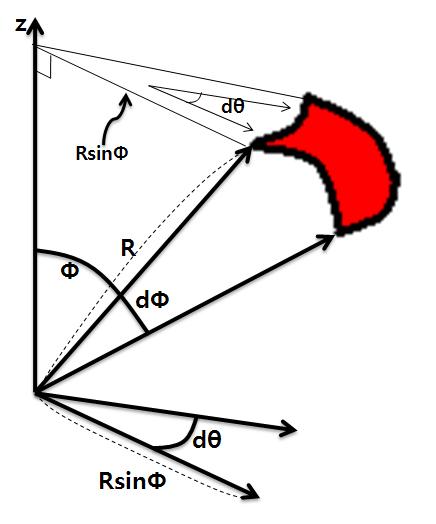
이제 이 도형의 각 변의 길이를 구해야하는데요.

부채꼴의 호의 길이를 구하는 공식으로 다음 공식이 있습니다.

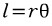
이를 위 그림에 적용하면,

미소입자의 각 변의 길이는 각각 RdΦ, RsinΦdθ 로 구해집니다.

따라서 입자의 넓이를 dS라고 두면, 

 

dS는 RdΦ와 RsinΦdθ의 곱입니다.

 

 

 

 

 

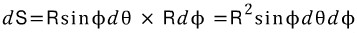
ii) 미소입자를 적분하기.

이제 위에서 구한 미소입자들을 한데 모아 더해봅시다.

각 위치별로 생기는 모든 입자들의 넓이의 합이 바로 구의 겉넓이가 될 것입니다.

 

앞에서 도입한 구형좌표계 그림을 가져와봅시다. 아래 그림은 전체 구의 1/8 부분만큼 해당하는 그림입니다. 그림에서 보이는 점이 미소입자를 구했던 위치입니다.

 

 

구 표면에 존재하는 모든 점들을 어떻게하면 표현할 수 있을까요?

구형좌표계의 θ와 Φ를 각각 0≤θ≤2π, 0≤Φ≤π 의 범위만큼 움직이하면 됩니다.

(이로써 구형좌표계를 도입한 이유를 설명할 수 있습니다. 데카르트 좌표계의 x, y, z로는 구 표면 위에 존재하는 모든 점을 x, y, z의 범위로 나타내기가 여간 까다로운 게 아닙니다.)

 

 

이제 모든 위치(0≤θ≤2π, 0≤Φ≤π )에서 생기는 모든 미소입자들의 합을 구해봅시다.

작은 요소 요소들을 더한다는 것은 적분의 개념입니다.

구 전체의 겉넓이를 S라 두면, 다음 수식을 세울 수 있습니다.

 

 

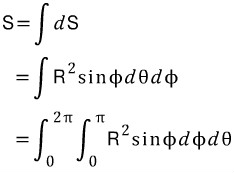
위에서 보이는 게 이중적분입니다.

이중적분은 별다른 게 아니라 차례차례 단일적분계산을 해주면 됩니다.

안쪽에 있는 적분을 먼저 해 줍시다.

이 결과를 이중적분속에 넣으면,

 

따라서 구의 겉넓이 S는 4πR² 임을 얻을 수 있습니다.

 

 

---

정리       

이번 포스팅에서는

구의 겉넓이 공식 유도를 해보았습니다.

 

그 과정에서 미분과 적분의 개념을, 다소 직관적인 방법으로 설명했습니다.

이처럼 어떤 도형의 넓이를 구한다는 것은

 

 i) 도형을 무수히 많은 미소입자로 잘게 쪼갠 뒤(미분)

ii) 그 미소입자의 넓이를 모두 합한다(적분)

 

는 뜻입니다.

구의 겉넓이를 구하는 과정은 고교 수학 범위를 넘어갑니다.

그러나 그 결과 (S=4πR² ) 만큼은 꼭 기억하고 있어야합니다.