타원의 넓이 구하기(치환적분)
타원의 넓이 구하기(치환적분)
이 포스팅은 타원의 넓이 유도에 관한 글 입니다.
고등학교 수학 기하와 벡터 파트에서는 타원의 정의, 장축, 단축, 초점, 접선에 대해 다루는데 타원의 넓이를 구하는 과정은 빠져있습니다.
이와 관련해 궁금한 학생들을 위하여 포스팅합니다.
이 글이 필요한 학생은
1. 타원의 넓이 구하는 방법이 궁금한 학생.
2. 타원의 넓이 공식이 궁금한 학생.
3. 이차곡선의 개념이 부족한 학생.
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
그럼 포스팅 시작합니다.
타원의 넓이
다음과 같은 타원의 방정식 표준형에 대하여,

타원의 넓이 S는 abπ 로 주어집니다.


증명
* 도형을 함수로 표현하기.
타원의 넓이를 구하기 위해선 타원의 '방정식'을 '함수'형태로 바꿔줘야 합니다.
(적분을 수행하기 위해선 방정식이 아닌 '함수'가 필요합니다.)
타원의 표준형을 y = f(x) 꼴로 바꾸면 다음과 같습니다.

타원의 방정식을 함수의 형태로 바꿔주면 이렇게 두 개(하나는 +, 하나는 -)의 함수로 표현가능합니다.
(일반적으로 x축 대칭인 도형의 방정식은 두 함수(하나는 x축 위(+), 하나는 x축 아래(-))로 표현가능합니다.)
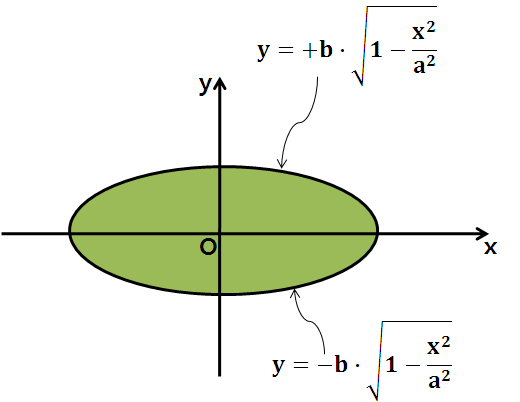
* 정적분의 범위 구하기(장축)
함수의 넓이는 정적분을 통해 구할 수 있는데요. 정적분을 하려면 적분범위가 주어져야 합니다.
위 그림에서는 적분범위가 타원의 장축이 되겠군요.
즉 타원이 x축과 만나는 부분 (y=0 일때의 x값)이 되겠는데요, 대입해보면 x=±a 를 얻을 수 있습니다.
따라서, 적분범위는 -a≤x≤+a 이며, 타원의 넓이 정적분은 아래와 같이 표현할 수 있습니다.

위에서 2를 곱한 이유는, 타원이 x축 대칭 도형이기 때문에 윗쪽함수(+b√(1-a²/x²)의 넓이만 구한 뒤 두 배를 해주면 넓이가 나오기 때문입니다.
식을 좀 정리하면 아래와 같습니다.

루트(√) 안의 함수가 우함수(y축 대칭)이기 때문에 적분범위 -a≤x≤+a 를 0≤x≤+a 로 바꿔주고 값을 두 배로 해줬습니다. (루트 안의 함수에 x대신 -x를 넣어도 함수가 같습니다. 따라서 위 함수는 f(-x) = f(x)가 되는 '우함수'입니다.)

* 치환적분
이제 실제 정적분값을 구해봅시다. 이 적분은 치환적분으로 쉽게 해낼 수 있습니다.
치환할 때 중요한 것은 변수의 범위변화 및 미소량(dx, dt) 간의 관계입니다.
삼각함수의 제곱공식 (sin²θ+cos²θ=1) 의 성질을 이용하기 위해 위 적분의 x를 asinθ로 치환합니다.
x = asinθ
이 때 변수 x의 범위가 0≤x≤a 일 때 치환된 변수 θ의 범위는 0≤θ≤π/2 가 됩니다. (x에 0과 a를 각각 대입해보세요. 그에 해당하는 각각의 θ를 얻을 수 있습니다.)
한편, 미소량 dx와 dθ의 관계는 「x=asinθ」의 양변을 x로 미분하면 얻을 수 있습니다.

이 결과를 위 정적분에 대입해봅시다.

마지막 등호에서 1-sin²θ=cos²θ를 이용했습니다.
특히 √cos²θ = lcosθl 로 나와야하지만 0≤θ≤π/2 에서는 cosθ가 양수이므로(그래프를 떠올려보세요.) 절댓값을 그대로 벗겨낼 수 있었습니다.
한편, 삼각함수 반각공식 중 코사인의 반각공식은 다음과 같습니다.

α대신 2θ로 바꾸어서 식에 대입하면 아래처럼 전개할 수 있습니다.

따라서 타원의 넓이는 S=abπ 로 주어집니다.
//유도완료
4. 정리
이번 포스팅에서는 타원의 넓이가 S=abπ로 주어짐을 알아보고 이를 유도 해보았습니다.
유도 과정에서
-도형을 함수로 표현하는 법.
-우함수, 기함수의 개념 및 이를 정적분에 적용하는 법.
-치환적분의 개념.
-삼각함수의 반각공식.
등 여러 개념을 복합적으로 적용했습니다.
타원의 넓이 유도는 교과과정에는 빠져있으나, 그간 배운 개념을 적용해보고 다시 한 번 점검해보는 데 유용해서 이렇게 소개했습니다.
제 글이 많은 학생에게 도움이 됐으면 합니다.